Отношение вершинной двусвязности — различия между версиями
(→Точки сочленения) |
(→Вершинная двусвязность) |
||
| Строка 5: | Строка 5: | ||
}} | }} | ||
Заметим, что если имеется два различных двусвязных ребра, то они лежат на некотором вершинно простом цикле. | Заметим, что если имеется два различных двусвязных ребра, то они лежат на некотором вершинно простом цикле. | ||
| − | + | ||
| + | |||
{{Теорема | {{Теорема | ||
|statement= | |statement= | ||
Версия 20:55, 25 сентября 2011
Вершинная двусвязность
| Определение: |
| Два ребра графа называются вершинно двусвязными, если существуют вершинно непересекающиеся пути, соединяющие их концы. |
Заметим, что если имеется два различных двусвязных ребра, то они лежат на некотором вершинно простом цикле.
| Теорема: |
Отношение вершинной двусвязности является отношением эквивалентности на ребрах. |
| Доказательство: |
|
Рефлексивность:
В данном случае имеем 2 пустых пути, которые, очевидно, не пересекаются.
|
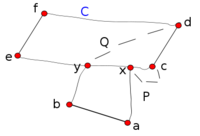
Замечание. Рассмотрим следующее определение: вершины и называются вершинно двусвязными, если между ними существуют 2 пути, не пересекающихся по вершинам, за исключением концов. Это определение не может претендовать на корректность, так как в этом случае отношение вершинной двусвязности перестанет быть транзитивным.
Блоки
| Определение: |
| Блоками, или компонентами вершинной двусвязности графа, называют его подграфы, множества ребер которых - классы эквивалентности вершинной двусвязности, а множества вершин - множества всевозможных концов ребер из соответствующих классов. |
Точки сочленения
| Определение: |
| Точка сочленения графа - вершина, принадлежащая как минимум двум блокам . |
| Определение: |
| Точка сочленения графа - вершина, при удалении которой в увеличивается число компонент связности. |