Построение по НКА эквивалентного ДКА, алгоритм Томпсона — различия между версиями
(→Алгоритм Томпсона) |
(→Построение эквивалентного ДКА по НКА) |
||
| Строка 44: | Строка 44: | ||
А это означает, что автоматы эквивалентны. | А это означает, что автоматы эквивалентны. | ||
}} | }} | ||
| + | |||
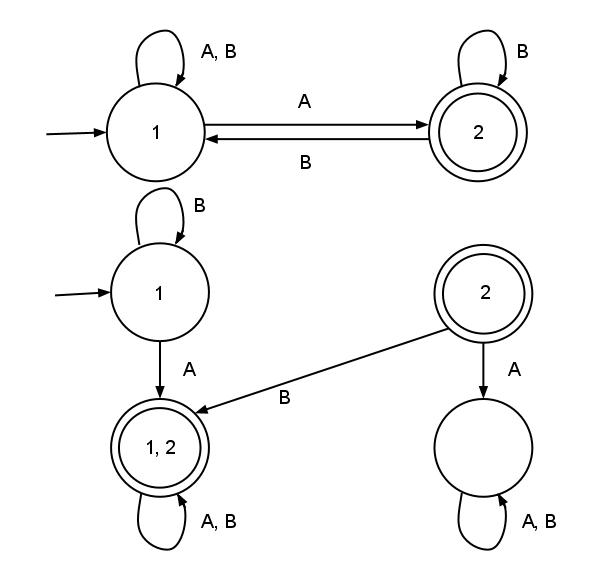
| + | ===Пример=== | ||
| + | [[Файл:DKA_NKA.jpg]] | ||
== Алгоритм Томпсона == | == Алгоритм Томпсона == | ||
Версия 22:51, 21 октября 2011
Содержание
Построение эквивалентного ДКА по НКА
НКА: .
ДКА, описанный в следующих строках является эквивалентным НКА.
ДКА: , где:
- .
- .
- .
- при условии, что .
Доказательство эквивалентности
| Теорема: |
Построенный ДКА эквивалентен данному НКА. |
| Доказательство: |
|
Докажем, что любое слово, которое принимает НКА, будет принято построенным ДКА. Сначала сделаем наблюдение, что если , и является символом перехода, то : . Рассмотрим слово w, которое принимает автомат НКА: , и . Проверим, что построенный ДКА тоже принимает это слово. Заметим, что , а, значит, исходя из нашего наблюдения мы получаем, что , где . Далее несложно заметить, что , где . Таким образом, , а из определения терминальных состояний в построенном ДКА мы получаем, что , а, значит, наш ДКА, тоже принимает cлово . Докажем, что любое слово, которое принимает построенный ДКА, принимает и НКА. Сначала сделаем наблюдение, что если , и мы из него достигли по строке какого-то состояния , то : существует путь из в в НКА по строке . Рассмотрим слово w, которое принимает автомат ДКА: , и . Проверим, что НКА тоже принимает это слово. А так как , и мы из достигли , возьмём любое терминальное состояние , то - по нашему наблюдению, в НКА есть путь из в по нужной строке, а, значит, что НКА принимает это слово. Получается, что мы доказали, что если НКА принимает слово, равносильно тому, что ДКА его тоже принимает. А это означает, что автоматы эквивалентны. |
Пример
Алгоритм Томпсона
Данный алгоритм преобразовывает НКА в эквивалентный ДКА. Мы будем использовать предыдущий способ построения с одним дополнением - нам не нужны состояния недостижимые из стартового.
Поэтому в алгоритме используется обход в ширину.
Алгоритм
- очередь состояний, соответствующих множествам, состоящих из состояний НКА. - стартовое состояние НКА.
1: 2: 3: 4: 5: 6: 7: 8: ) 9: 10: 11:
Верхняя оценка на работу алгоритмы - - так как количество подмножеств множества состояний НКА не более, чем , а каждое подмножество мы обрабатываем за и ровно один раз.