Основные определения теории графов — различия между версиями
Baev.dm (обсуждение | вклад) |
Baev.dm (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
{{В разработке}} | {{В разработке}} | ||
==Ориентированные графы (directed graph)== | ==Ориентированные графы (directed graph)== | ||
| − | |||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | Ориентированным графом <tex>G</tex> называется пара <tex>G = (V, E)</tex>, где <tex>V</tex> - конечное множество вершин, а <tex> E \subset V \times V </tex> - множество рёбер. | + | '''Ориентированным графом''' <tex>G</tex> называется пара <tex>G = (V, E)</tex>, где <tex>V</tex> - конечное множество вершин, а <tex> E \subset V \times V </tex> - множество рёбер. |
}} | }} | ||
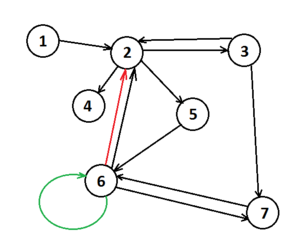
| − | [[Файл: | + | [[Файл: directed_graph.png|thumb|300px|right|Ориентированный граф<br><font color=#ED1C24>Красным</font> выделено ребро (6, 2)<br><font color=#22B14C>Зеленым</font> обозначена петля (6, 6)]] |
| − | + | ||
| − | Ориентированным графом <tex>G</tex> называется четверка <tex>G = (V, E, beg, end)</tex> , где <tex>beg, end : E \rightarrow V </tex>, а <tex>V</tex> и <tex>E</tex> - некоторые абстрактные множества. Иногда граф, построенный таким образом называют '''мультиграфом'''. В мультиграфе не допускаются петли (см. определение ниже), но пары вершин допускается соединять более чем одним ребром. Такие ребра называются '''кратными''' (иначе - '''параллельные'''). | + | Заметим, что по такому определению любые две вершины <tex>u,~v</tex> нельзя соединить более чем одним ребром <tex>(u, v)</tex>. |
| + | Поэтому часто используют немного другое определение. | ||
| + | |||
| + | '''Ориентированным графом''' <tex>G</tex> называется четверка <tex>G = (V, E, beg, end)</tex> , где <tex>beg, end : E \rightarrow V </tex>, а <tex>V</tex> и <tex>E</tex> - некоторые абстрактные множества. Иногда граф, построенный таким образом называют '''мультиграфом'''. В мультиграфе не допускаются петли (см. определение ниже), но пары вершин допускается соединять более чем одним ребром. Такие ребра называются '''кратными''' (иначе - '''параллельные'''). | ||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | Ребром (дугой) ориентированного графа называют упорядоченную пару вершин <tex> (v, u) \in E </tex>. | + | '''Ребром''' (дугой) ориентированного графа называют упорядоченную пару вершин <tex> (v, u) \in E </tex>. |
}} | }} | ||
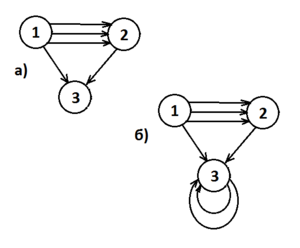
| + | [[Файл: Multigraph.png|thumb|300px|right|а) мультиграф<br> б) псевдограф]] | ||
| + | |||
| + | В ориентированном графе ребро, концы которого совпадают, то есть <tex>e=\{v,v\}</tex>, называется <b>петлей</b>. Мультиграф с петлями принято называть '''псевдографом'''. | ||
| − | |||
Если имеется ребро <tex> (v, u) \in E </tex>, то иногда говорят, что <tex> u </tex> - <b>родитель</b> <tex> v </tex>. Также вершины <tex> u </tex> и <tex> v </tex> называют <b>смежными</b>. Граф с <tex> p </tex> вершинами и <tex> q </tex> ребрами называют <tex> (p, q) </tex> - графом. <tex> (1, 0) </tex> - граф называют <b>тривиальным</b>. | Если имеется ребро <tex> (v, u) \in E </tex>, то иногда говорят, что <tex> u </tex> - <b>родитель</b> <tex> v </tex>. Также вершины <tex> u </tex> и <tex> v </tex> называют <b>смежными</b>. Граф с <tex> p </tex> вершинами и <tex> q </tex> ребрами называют <tex> (p, q) </tex> - графом. <tex> (1, 0) </tex> - граф называют <b>тривиальным</b>. | ||
| − | + | Так же еще для ориентированных графов определяют '''полустепень входа вершины'''. | |
| − | + | ||
| − | + | <tex>deg^-v_i = |\{e~|beg~e = v\}|</tex>.<br> | |
| − | + | <tex>deg^+v_i = |\{e~|end~e = v\}|</tex>.<br> | |
| − | + | ||
| + | Докажем, что выполнено следующее равенство: | ||
| + | |||
| + | <tex>\sum\limits_{v\in V(G)}deg^-v_i = \sum\limits_{v\in V(G)}deg^+v_i = |E|</tex>.<br> | ||
| + | |||
| + | У каждого ребра ровно одно начало и ровно один конец. | ||
{{Определение | {{Определение | ||
Версия 03:59, 26 октября 2011
Ориентированные графы (directed graph)
| Определение: |
| Ориентированным графом называется пара , где - конечное множество вершин, а - множество рёбер. |
Заметим, что по такому определению любые две вершины нельзя соединить более чем одним ребром . Поэтому часто используют немного другое определение.
Ориентированным графом называется четверка , где , а и - некоторые абстрактные множества. Иногда граф, построенный таким образом называют мультиграфом. В мультиграфе не допускаются петли (см. определение ниже), но пары вершин допускается соединять более чем одним ребром. Такие ребра называются кратными (иначе - параллельные).
| Определение: |
| Ребром (дугой) ориентированного графа называют упорядоченную пару вершин . |
В ориентированном графе ребро, концы которого совпадают, то есть , называется петлей. Мультиграф с петлями принято называть псевдографом.
Если имеется ребро , то иногда говорят, что - родитель . Также вершины и называют смежными. Граф с вершинами и ребрами называют - графом. - граф называют тривиальным.
Так же еще для ориентированных графов определяют полустепень входа вершины.
.
.
Докажем, что выполнено следующее равенство:
.
У каждого ребра ровно одно начало и ровно один конец.
| Определение: |
| Путём в графе называется последовательность вида , где . |
| Определение: |
| Циклическим путём называется путь, в котором . |
| Определение: |
| Цикл - это класс эквивалентности циклических путей на отношении эквивалентности таком, что два пути эквивалентны, если ; где и - это две последовательности ребер в циклическом пути. |