Теорема о существовании простого цикла в случае существования цикла — различия между версиями
Baev.dm (обсуждение | вклад) |
Baev.dm (обсуждение | вклад) |
||
| Строка 14: | Строка 14: | ||
}} | }} | ||
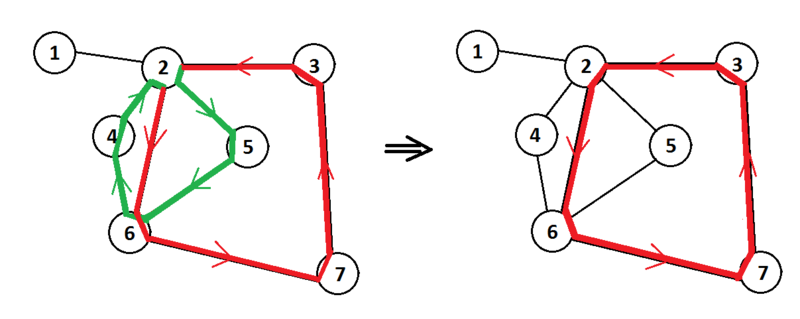
| − | [[Файл: prime_c.png|thumb|center|Для вершины 2 находим последнее ее вхождение в цикл и удаляем отрезок цикла (2, 5)-5-(5, 6)-6-(6, 4)-2]] | + | [[Файл: prime_c.png|thumb|800px|center|Для вершины 2 находим последнее ее вхождение в цикл и удаляем отрезок цикла (2, 5)-5-(5, 6)-6-(6, 4)-4-(4, 2)-2]] |
| + | |||
== Замечания == | == Замечания == | ||
* Наличие двух различных рёберно-простых путей между какими-либо вершинами графа равносильно наличию цикла в этом графе. | * Наличие двух различных рёберно-простых путей между какими-либо вершинами графа равносильно наличию цикла в этом графе. | ||
Версия 03:42, 27 октября 2011
| Теорема: |
Если между двумя вершинами неориентированного графа существуют два различных рёберно-простых пути, то в этом графе существует простой цикл. |
| Доказательство: |
|
Возьмём два существующих пути между нужными нам вершинами: , , , . Удалим из путей одинаковые префиксы и суффиксы, оставив из тех только последние и первые вершины, соответственно. Оставшиеся пути: , , , , , . Рассмотрим конкатенацию первого нового пути и развёрнутого второго нового пути. Она будет циклом, так как начальная и конечная вершины совпадают, изначально пути были рёберно-простыми, а в точке соединения, равно как и в точке замыкания цикла, условие различности двух идущих подряд рёбер выполняется. Мы получили цикл, определим его: , .
1. Для вершины найдём момент её последнего вхождения в цикл – . 2. Удалим отрезок цикла от до , включительно. Получившаяся последовательность вершин и рёбер графа останется циклом, и в нём вершина будет содержаться ровно один раз.Начнём процесс с вершины и будем повторять его каждый раз для следующей вершины нового цикла, пока не дойдём до последней. По построению, получившийся цикл будет содержать каждую из вершин графа не более одного раза, а значит, будет простым. |
Замечания
- Наличие двух различных рёберно-простых путей между какими-либо вершинами графа равносильно наличию цикла в этом графе.
- Так как вершинно-простой путь всегда является рёберно-простым, данная теорема справедлива и для вершинно-простых путей (усиление условия).
- Так как вершинно-простой цикл всегда является рёберно-простым, данная теорема справедлива и для рёберно-простого цикла (ослабление результата).
- Утверждение
Если две вершины графа лежат на цикле, то они лежат на простом цикле.
в общем случае неверно, так как эти вершины могут лежать в разных компонентах вершинной или рёберной двусвязности: все пути из одной вершины в другую будут содержать одну и ту же точку сочленения или один и тот же мост.