Граф блоков-точек сочленения — различия между версиями
Creep (обсуждение | вклад) |
Creep (обсуждение | вклад) |
||
| Строка 16: | Строка 16: | ||
}} | }} | ||
==Литература== | ==Литература== | ||
| − | + | ||
== См. также == | == См. также == | ||
* [[Граф компонент реберной двусвязности]] | * [[Граф компонент реберной двусвязности]] | ||
Версия 22:45, 28 октября 2011
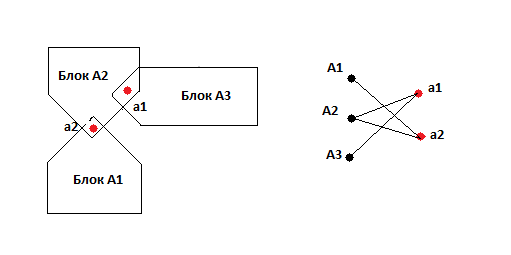
| Определение: |
| Пусть граф связен. Обозначим - блоки, а - точки сочленения . Построим двудольный граф , поместив и в различные его доли. Если точка сочленения принадлежит блоку, проведем между ними ребро. Полученный граф называют графом блоков-точек сочленения графа . |
| Лемма: |
В определении, приведенном выше, - дерево. |
| Доказательство: |
|
Достаточно показать, что в нет циклов. Пусть - последовательные вершины , лежащие на цикле. Тогда существует последовательность точек сочленения и блоков, соединяющая и и не содержащая . По ней можно проложить путь в (можем переходить из блока в блок по точке сочленения и из одной части блока в другую) и замкнуть его в вершине , получив цикл, что противоречит тому, что - точка сочленения. Пусть аналогично - лежащие на цикле последовательные вершины . В этом случае рассуждение такое же, и и не смогут быть точками сочленения из-за цикла в . |