Минимизация ДКА, алгоритм за O(n^2) с построением пар различимых состояний

Определения

Определение:

Состояния [math]u[/math] и [math]v[/math] различимы строкой [math]s[/math] если [math] \langle u, s \rangle \vdash^* \langle t, \varepsilon \rangle [/math], где [math]t \in T [/math] [math] \langle v, s \rangle \vdash^* \langle z, \varepsilon \rangle [/math], где [math]z \notin T [/math]

Определение:

Состояния [math]u[/math] и [math]v[/math] эквивалентны, если они неразличимы никакой строкой [math]s[/math].

Теорема:

Если [math]u[/math] и [math]v[/math], [math]v[/math] и [math]z[/math] эквивалентны, то [math]u[/math] и [math]z[/math] эквивалентны.

Доказательство:

[math]\triangleright[/math]

Пусть [math]u[/math] и [math]z[/math] неэквивалентны. Тогда [math] \mathcal {9} s[/math], такой, что [math] \langle u, s \rangle \vdash^* \langle t, \varepsilon \rangle [/math], где [math]t \in T [/math] [math] \langle z, s \rangle \vdash^* \langle t_1, \varepsilon \rangle [/math], где [math]t_1 \notin T [/math]. Рассмотрим [math]x[/math], такой, что [math] \langle v, s \rangle \vdash^* \langle x, \varepsilon \rangle [/math]. Если [math]x \in T[/math], то [math]v[/math] и [math]z[/math] различимы строкой [math]s[/math]. Противоречие. Если [math]x \notin T[/math], то [math]u[/math] и [math]v[/math] различимы строкой [math]s[/math]. Противоречие. Значит, [math]u[/math] и [math]z[/math] эквивалентны.

[math]\triangleleft[/math]

Алгоритм

Основная идея алгоритма разбить состояния на классы эквивалентности — они и будут состояниями минимального автомата. В таблице размером [math]n \times n[/math], где [math]n[/math] — количество состояний автомата будем помечать неэквивалентные состояния. Изначально добавим в очередь [math]Q[/math] пары состояний различимых строкой [math] \varepsilon [/math] и пометим их в таблице. Пока [math]Q[/math] не станет пуста, будем делать следующее:

1. Извлечем пару [math] \langle u, v \rangle [/math] из [math]Q[/math].
2. Для всех пар [math] \langle t, k \rangle [/math], таких, что [math] \mathcal {9} c \in \Sigma, \langle t, c \rangle \vdash \langle u, \varepsilon \rangle, \langle k, c \rangle \vdash \langle v, \varepsilon \rangle [/math] и пара [math] \langle t, k \rangle[/math] не отмечена в таблице, то отметим ее в таблице и добавим в [math]Q[/math].

За один проход по таблице согласно теореме разбиваем не помеченные состояния на классы эквивалентности.

Корректность алгоритма

Пусть в результате применения данного алгоритма к автомату [math]A[/math] мы получили автомат [math]A_{min}[/math]. Докажем, что этот автомат минимальный и единственный с точностью до изоморфизма.
Пусть существует автомат [math]A'[/math] эквивалентный [math]A[/math], но с числом состояний меньшим чем в [math]A_{min}[/math]. Стартовые состояния [math]s \in A_{min}[/math] и [math]s' \in A'[/math] эквивалентны, так как [math]A_{min}[/math] и [math]A'[/math] допускают один и тот же язык. Рассмотрим строку [math]\alpha = a_1a_2...a_{k}[/math], где [math]a_{i} \in \Sigma[/math], такую что [math] \langle s, \alpha \rangle \vdash^* \langle u, \varepsilon \rangle [/math], [math] \langle s', \alpha \rangle \vdash^* \langle u', \varepsilon \rangle [/math]. Пусть [math]\langle s, a_1 \rangle \vdash^* \langle l, \varepsilon \rangle [/math] и [math]\langle s', a_1 \rangle \vdash^* \langle l', \varepsilon \rangle [/math]. Так как [math]s[/math] и [math]s'[/math] эквивалентны, то [math]l[/math] и [math]l'[/math] эквивалентны. Аналогично для всех [math]a_{i}[/math]. В итоге получим, что [math]u[/math] эквивалентно [math]u'[/math]. Значит для каждого состояния из [math]A_{min}[/math] существует эквивалентное состояние из [math]A'[/math]
Состояний в [math]A'[/math] меньше чем в [math]A_{min}[/math], значит двум состояниям из [math]A_{min}[/math] эквивалентно одно состояние из [math]A'[/math]. Тогда эти два состояния эквивалентны, но автомат [math]A_{min}[/math] построен так, что в нем нет эквивалентных состояний. Противоречие.
Так как каждому состоянию из [math]A_{min}[/math] эквивалентно состояние из [math]A'[/math], то автоматы [math]A_{min}[/math] и [math]A'[/math] изоморфны.

Время работы алгоритма

Каждую пару мы добавляли в очередь один раз, значит время заполнения таблицы [math]O(n^2)[/math]. Разбиение на классы эквивалентности делается за один проход по таблице, то есть за [math]O(n^2)[/math].

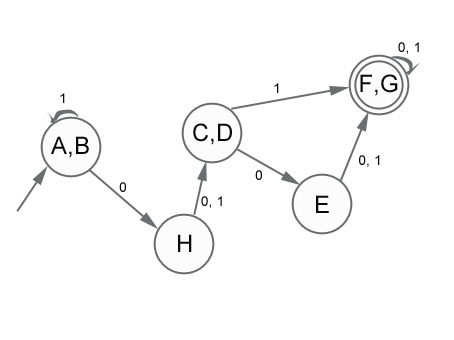
Пример

Минимизируем данный автомат.

Будем рассматривать только нижний треугольник таблицы пар различимых состояний.
Отметили состояния, различающиеся строкой [math]\varepsilon[/math]

B
C
D
E
F	x	x	x	x	x
G	x	x	x	x	x
H						x	x
	A	B	C	D	E	F	G

На момент опустошения очереди

B
C	x	x
D	x	x
E	x	x	x	x
F	x	x	x	x	x
G	x	x	x	x	x
H	x	x	x	x	x	x	x
	A	B	C	D	E	F	G

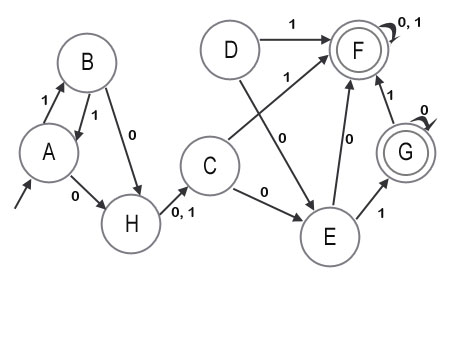
Из таблицы видно, что классы эквивалентных состояний это [math] \mathcal {f} A, B \mathcal {g}, \mathcal {f} C, D \mathcal {g}, \mathcal {f} F, G \mathcal {g}, \mathcal {f} E \mathcal {g}, \mathcal {f} H \mathcal {g} [/math].
Итого получили такой автомат: