Лемма о разрастании для КС-грамматик

{{Лемма |id= ==lemma== |about=о разрастании КС-грамматик |statement= Пусть [math]L[/math] — контекстно-свободный язык над алфавитом [math]\Sigma[/math], тогда существует такое [math]n[/math], что для любого слова [math] \omega \in L[/math] длины не меньше [math]n[/math] найдутся слова [math] u,v,x,y,z \in \Sigma^*[/math], для которых верно: [math]uvxyz=\omega, vy\neq \varepsilon, |vxy|\leqslant n[/math] и [math]\forall k \geqslant 0~uv^{k}xy^{k}z\in L[/math]. |proof=

Пусть [math]L[/math] — контекстно-свободный язык над алфавитом [math]\Sigma[/math]. Тогда его грамматика может быть записана в нормальной форме Хомского (НФХ). Пусть [math]m[/math] — количество нетерминалов в полученной грамматике.

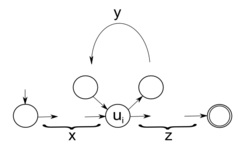
Выберем [math]n=2^{m}[/math]. Построим дерево разбора слова [math]\omega[/math]. Так как из одного нетерминала выводится либо два нетерминала, либо терминальный символ, то дерево разбора [math]\omega[/math] будет бинарным, причем его высота не меньше [math]m[/math]. Следовательно, по принципу Дерихле найдется такой нетерминал [math]A[/math], который раскрывается в дереве разбора дважды. Если таких нетерминалов несколько, то выберем нетерминал максимальной глубины, у которого в поддереве содержится такой же нетерминал. Тогда в качестве [math]x[/math] выберем кратчайшую строку из терминалов, которая выводится из [math]A[/math].