Использование обхода в глубину для поиска точек сочленения

Задача

Дан связный неориентированный граф. Требуется найти все точки сочленения в нем.

Алгоритм

Теорема:

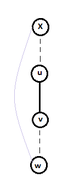
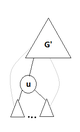
Пусть [math]T[/math] - дерево обхода в глубину, [math]root[/math] - корень [math]T[/math]. Вершина [math]u \ne root[/math] - точка сочленения [math]\Leftrightarrow \exists v \in T[/math] - сын [math]u[/math] : из [math]v[/math] или любого потомка вершины [math]v[/math] нет обратного ребра в предка вершины [math]u[/math]. [math]root[/math] - точка сочленения [math]\Leftrightarrow root[/math] имеет хотя бы двух сыновей в дереве поиска в глубину.

Доказательство:

[math]\triangleright[/math]

[math]\Leftarrow[/math] пункт 1 [math]\Leftarrow[/math] Удалим [math]u[/math] из [math]G[/math]. Докажем, что [math]\nexists[/math] пути из [math]v[/math] в любого предка вершины [math]u[/math]. Пусть это не так. Тогда [math]\exists x \in T[/math] - предок [math]u[/math] : [math]\exists[/math] путь из [math]v[/math] в [math]x[/math] в [math]G \backslash u[/math]. Пусть [math]w[/math] - предпоследняя вершина на этом пути, [math]w[/math] - потомок [math]v[/math]. [math](w, x)[/math] - не ребро дерева [math]T[/math](в силу единственности пути в дереве) [math]\Rightarrow (w, x)[/math] - обратное ребро, что противоречит условию. Пусть [math]root[/math] - точка сочленения и у него есть только 1 сын. Тогда при удалении [math]root[/math] остается дерево с корнем в его сыне, содержащее все остальные вершины графа, то есть оставшийся граф связен - противоречие с тем, что [math]root[/math] - точка сочленения. [math]\Rightarrow[/math] пункт 1 [math]\Rightarrow[/math] Докажем что из отрицания второго утверждения следует отрицание первого. Обозначим через [math]G'[/math] граф, состоящий из вершин, не являющихся потомками [math]u[/math]. Удалим вершину [math]u[/math]. Очевидно, что граф [math]G'[/math] и все поддеревья вершины [math]u[/math] останутся связными, кроме того из каждого поддерева есть ребро в [math]G' \Rightarrow G \backslash u[/math] - связный [math]\Rightarrow u[/math] - не точка сочленения. Пусть у [math]root[/math] хотя бы два сына. Тогда при удалении [math]root \, \nexists[/math] пути между его поддеревьями, так как не существует перекрестных ребер [math]\Rightarrow root[/math] - точка сочленения.

[math]\triangleleft[/math]

Пусть [math]tin[u][/math] - время входа поиска в глубину в вершину [math]u[/math]. Через [math]up[u][/math] обозначим минимум из времени захода в саму вершину [math]tin[u][/math], времен захода в каждую из вершин [math]p[/math], являющуюся концом некоторого обратного ребра [math](u,p)[/math], а также из всех значений [math]up[v][/math] для каждой вершины [math]v[/math], являющейся непосредственным сыном [math]u[/math] в дереве поиска.

Тогда, из вершины [math]u[/math] или её потомка есть обратное ребро в её предка [math]\Leftrightarrow \exists[/math] такой сын [math]v[/math], что [math]up[v] \lt tin[u][/math].

Таким образом, если для текущей вершины [math]v \ne root \, \exists[/math] непосредственный сын [math]v[/math]: [math]up[v] \ge tin[u][/math], то вершина [math]u[/math] является точкой сочленения; в противном случае она точкой сочленения не является.

Реализация

bool used[];
int tin[];
int up[];
bool answer[];                              //для каждой вершины содержится булево значение - является она точкой сочленения или нет. изначально все значения false
int time;

void dfs(int u, int prev)
{
    used[u] = true;
    tin[u] = up[u] = time++;                //задание времени входа tin и начального значения up для вершины u
    int count = 0;                          //счетчик количества детей вершины u в дереве обхода
    for (v : uv из E)
    {
        if (v == prev)
            continue;
        if (used[v])                        //v - предок вершины u, uv - обратное ребро
            up[u] = min(up[u], tin[v]);
        else                                //v - ребенок вершины u
        {
            ++count;
            dfs(v, u);
            up[u] = min(up[u], up[v]);
            if (up[v] >= tin[u])
                answer[u] = true;           //не существует обратного ребра из вершины v или ее потомка в предка вершины u. вершина u - точка сочленения
        }
    }
    if (prev == -1)                         //является ли u корнем дерева обхода
        answer[u] = (count > 1);            //проверка количества детей у корня дерева
}

int main()
{
    ...                                     //инициализация графа, выбор корня дерева обхода root
    time = 0;
    dfs(root, -1);
    return 0;
}

Для поиска точек сочленения в несвязном графе, необходимо модифицировать функцию main следующим образом:

int main()
{
    ...
    for (root из V)
        if (!used[root])
        {
            time = 0;
            dfs(root, -1);
        }
    return 0;
}

Источники

Асанов М., Баранский В., Расин В. - Дискретная математика: Графы, матроиды, алгоритмы — Ижевск: ННЦ "Регулярная и хаотическая динамика", 2001, 288 стр.