Использование обхода в глубину для поиска точек сочленения — различия между версиями
Dimitrova (обсуждение | вклад) |
Dimitrova (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
| − | + | [[Категория: Обход в глубину]] | |
| + | = Алгоритм = | ||
Дан [[Отношение связности, компоненты связности|связный]] [[Основные определения теории графов|неориентированный граф]]. Требуется найти все [[Точка сочленения, эквивалентные определения|точки сочленения]] в нем. | Дан [[Отношение связности, компоненты связности|связный]] [[Основные определения теории графов|неориентированный граф]]. Требуется найти все [[Точка сочленения, эквивалентные определения|точки сочленения]] в нем. | ||
| Строка 6: | Строка 7: | ||
Пусть <tex>T</tex> - дерево [[Обход в глубину, цвета вершин|обхода в глубину]], <tex>root</tex> - корень <tex>T</tex>. Вершина <tex>u \ne root</tex> - точка сочленения <tex>\Leftrightarrow \exists v \in T</tex> - сын <tex>u</tex> : из <tex>v</tex> или любого потомка вершины <tex>v</tex> нет обратного ребра в предка вершины <tex>u</tex>. <tex>root</tex> - точка сочленения <tex>\Leftrightarrow root</tex> имеет хотя бы двух сыновей в дереве поиска в глубину. | Пусть <tex>T</tex> - дерево [[Обход в глубину, цвета вершин|обхода в глубину]], <tex>root</tex> - корень <tex>T</tex>. Вершина <tex>u \ne root</tex> - точка сочленения <tex>\Leftrightarrow \exists v \in T</tex> - сын <tex>u</tex> : из <tex>v</tex> или любого потомка вершины <tex>v</tex> нет обратного ребра в предка вершины <tex>u</tex>. <tex>root</tex> - точка сочленения <tex>\Leftrightarrow root</tex> имеет хотя бы двух сыновей в дереве поиска в глубину. | ||
|proof= | |proof= | ||
| − | [[Файл:Поиск точек сочелнения.png|thumb| | + | [[Файл:Поиск точек сочелнения.png|thumb|50px]] |
<tex>\Leftarrow</tex> | <tex>\Leftarrow</tex> | ||
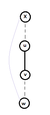
#Удалим <tex>u</tex> из <tex>G</tex>. Докажем, что <tex>\nexists</tex> пути из <tex>v</tex> в любого предка вершины <tex>u</tex>. Пусть это не так. Тогда <tex>\exists x \in T</tex> - предок <tex>u</tex> : <tex>\exists</tex> путь из <tex>v</tex> в <tex>x</tex> в <tex>G \backslash u</tex>. Пусть <tex>w</tex> - предпоследняя вершина на этом пути, <tex>w</tex> - потомок <tex>v</tex>. <tex>(w, x)</tex> - не ребро дерева <tex>T</tex>(в силу единственности пути в дереве) <tex>\Rightarrow (w, x)</tex> - обратное ребро, что противоречит условию. | #Удалим <tex>u</tex> из <tex>G</tex>. Докажем, что <tex>\nexists</tex> пути из <tex>v</tex> в любого предка вершины <tex>u</tex>. Пусть это не так. Тогда <tex>\exists x \in T</tex> - предок <tex>u</tex> : <tex>\exists</tex> путь из <tex>v</tex> в <tex>x</tex> в <tex>G \backslash u</tex>. Пусть <tex>w</tex> - предпоследняя вершина на этом пути, <tex>w</tex> - потомок <tex>v</tex>. <tex>(w, x)</tex> - не ребро дерева <tex>T</tex>(в силу единственности пути в дереве) <tex>\Rightarrow (w, x)</tex> - обратное ребро, что противоречит условию. | ||
#Пусть <tex>root</tex> - точка сочленения и у него есть только 1 сын. Тогда при удалении <tex>root</tex> остается дерево с корнем в его сыне, содержащее все остальные вершины графа, то есть оставшийся граф связен - противоречие с тем, что <tex>root</tex> - точка сочленения. | #Пусть <tex>root</tex> - точка сочленения и у него есть только 1 сын. Тогда при удалении <tex>root</tex> остается дерево с корнем в его сыне, содержащее все остальные вершины графа, то есть оставшийся граф связен - противоречие с тем, что <tex>root</tex> - точка сочленения. | ||
| − | + | [[Файл:Поиск точек сочеленения1.png|thumb|60px]] | |
| − | |||
| − | |||
| − | [[Файл:Поиск точек сочеленения1.png|thumb| | ||
<tex>\Rightarrow</tex> | <tex>\Rightarrow</tex> | ||
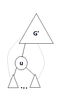
#Докажем что из отрицания второго утверждения следует отрицание первого. Обозначим через <tex>G'</tex> граф, состоящий из вершин, не являющихся потомками <tex>u</tex>. Удалим вершину <tex>u</tex>. Очевидно, что граф <tex>G'</tex> и все поддеревья вершины <tex>u</tex> останутся связными, кроме того из каждого поддерева есть ребро в <tex>G' \Rightarrow G \backslash u</tex> - связный <tex>\Rightarrow u</tex> - не точка сочленения. | #Докажем что из отрицания второго утверждения следует отрицание первого. Обозначим через <tex>G'</tex> граф, состоящий из вершин, не являющихся потомками <tex>u</tex>. Удалим вершину <tex>u</tex>. Очевидно, что граф <tex>G'</tex> и все поддеревья вершины <tex>u</tex> останутся связными, кроме того из каждого поддерева есть ребро в <tex>G' \Rightarrow G \backslash u</tex> - связный <tex>\Rightarrow u</tex> - не точка сочленения. | ||
| Строка 26: | Строка 24: | ||
Таким образом, если для текущей вершины <tex>v \ne root \, \exists</tex> непосредственный сын <tex>v</tex>: <tex>up[v] \ge tin[u]</tex>, то вершина <tex>u</tex> является точкой сочленения; в противном случае она точкой сочленения не является. | Таким образом, если для текущей вершины <tex>v \ne root \, \exists</tex> непосредственный сын <tex>v</tex>: <tex>up[v] \ge tin[u]</tex>, то вершина <tex>u</tex> является точкой сочленения; в противном случае она точкой сочленения не является. | ||
| − | == | + | = Время Работы = |
| − | + | Время работы алгоритма совпадает с временем работы <tex> dfs </tex>. Он равен <tex> O(V + E) </tex> | |
| − | + | ||
| − | + | = Реализация = | |
| − | |||
| − | |||
| − | + | dfs(<tex>u</tex>, <tex>prev</tex>) | |
| − | + | Помечаем вершину <tex>u</tex>, как посещенную | |
| − | + | <tex>tin[u] \leftarrow up[u] \leftarrow time</tex>++ | |
| − | tin[u] | + | <tex>count \leftarrow</tex> 0 |
| − | + | for (<tex>v</tex> : <tex>uv</tex> из <tex>E</tex>) | |
| − | for (v : uv из E) | + | if (<tex>v</tex> родитель <tex>u</tex>) |
| − | + | Переходим к следующей итерации цикла | |
| − | if (v | + | if (<tex>v</tex> посещено) //v - предок вершины u, uv - обратное ребро |
| − | + | <tex>up[u] \leftarrow min(up[u], tin[v])</tex> | |
| − | if ( | ||
| − | up[u] | ||
else //v - ребенок вершины u | else //v - ребенок вершины u | ||
| − | + | <tex>count</tex>++ | |
| − | ++ | + | dfs(<tex>v, u</tex>) |
| − | dfs(v, u) | + | <tex>up[u] \leftarrow min(up[u], up[v])</tex> |
| − | up[u] | + | if (<tex>up[v]</tex> >= <tex>tin[u]</tex>) |
| − | if (up[v] >= tin[u]) | + | <tex>answer[u] \leftarrow true</tex> |
| − | answer[u] | + | if (<tex>u</tex> корень) |
| − | + | <tex>answer[u] \leftarrow (count > 1)</tex> | |
| − | |||
| − | if ( | ||
| − | answer[u] | ||
| − | |||
| − | + | main() | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
... | ... | ||
| − | for (root из V) | + | for (<tex>root</tex> из <tex>V</tex>) |
| − | if ( | + | if (<tex>root</tex> не посещен) |
| − | + | <tex>time \leftarrow 0</tex> | |
| − | time | + | dfs(<tex>root</tex>, -1); |
| − | dfs(root, -1); | ||
| − | |||
| − | |||
| − | |||
| − | + | = Источники = | |
Асанов М., Баранский В., Расин В. - Дискретная математика: Графы, матроиды, алгоритмы — Ижевск: ННЦ "Регулярная и хаотическая динамика", 2001, 288 стр. | Асанов М., Баранский В., Расин В. - Дискретная математика: Графы, матроиды, алгоритмы — Ижевск: ННЦ "Регулярная и хаотическая динамика", 2001, 288 стр. | ||
Версия 20:54, 25 ноября 2011
Содержание
Алгоритм
Дан связный неориентированный граф. Требуется найти все точки сочленения в нем.
| Теорема: |
Пусть - дерево обхода в глубину, - корень . Вершина - точка сочленения - сын : из или любого потомка вершины нет обратного ребра в предка вершины . - точка сочленения имеет хотя бы двух сыновей в дереве поиска в глубину. |
| Доказательство: |
|
|
Пусть - время входа поиска в глубину в вершину . Через обозначим минимум из времени захода в саму вершину , времен захода в каждую из вершин , являющуюся концом некоторого обратного ребра , а также из всех значений для каждой вершины , являющейся непосредственным сыном в дереве поиска.
Тогда, из вершины или её потомка есть обратное ребро в её предка такой сын , что .
Таким образом, если для текущей вершины непосредственный сын : , то вершина является точкой сочленения; в противном случае она точкой сочленения не является.
Время Работы
Время работы алгоритма совпадает с временем работы . Он равен
Реализация
dfs(, ) Помечаем вершину , как посещенную ++ 0 for ( : из ) if ( родитель ) Переходим к следующей итерации цикла if ( посещено) //v - предок вершины u, uv - обратное ребро else //v - ребенок вершины u ++ dfs() if ( >= ) if ( корень) main() ... for ( из ) if ( не посещен) dfs(, -1);
Источники
Асанов М., Баранский В., Расин В. - Дискретная математика: Графы, матроиды, алгоритмы — Ижевск: ННЦ "Регулярная и хаотическая динамика", 2001, 288 стр.