Алгоритм Кока-Янгера-Касами разбора грамматики в НФХ

Пусть дана контекстно-свободная грамматика грамматика [math]\Gamma[/math] и слово [math]w \in \Sigma^{*}[/math]. Требуется выяснить, выводится ли это слово в данной грамматике.

Алгоритм для НФХ-грамматики

Пусть [math]\Gamma[/math] приведена к нормальной форме Хомского.

Пусть [math]a_{A, i, j} = true[/math], если из нетерминала [math]A[/math] можно вывести подстроку [math]w[i..j][/math]. Иначе [math]a_{A, i, j} = false[/math]:

[math]a_{A, i, j} = \begin{cases} true,&\text{$A \Rightarrow^{*} w[i..j]$;}\\ false,&\text{else.} \end{cases} [/math].

Будем динамически заполнять матрицу [math]a_{A, i, j}[/math] следующим алгоритмом:

• База. Ячейки [math]a_{A, i, i}[/math] заполняются истиной, если правило [math]A \rightarrow w[i][/math] принадлежит множеству правил [math]P[/math] грамматики [math]\Gamma[/math]:

[math]a_{A, i, i} = \lbrack A \rightarrow w[i] \in P \rbrack[/math].

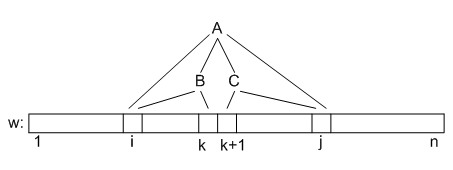
• Переход. Пусть на текущем шаге [math]j-i=m\gt 0[/math]. Если все ячейки, для которых справедливо [math]j-i\lt m[/math], уже вычислены, то алгоритм смотрит, можно ли вывести подстроку [math]w[i..j][/math] из этих ячеек:

[math]a_{A, i, j} = \bigvee\limits_{k=i}^{j-1} \bigvee\limits_{A \rightarrow BC} \left( a_{B, i, k} \wedge a_{C, k+1, j} \right)[/math].

• Завершение. После окончания работы ответ содержится в ячейке [math]a_{S, 1, n}[/math], где [math]n = |w|[/math].

Сложность алгоритма

Необходимо вычислить [math]n^2[/math] булевых величин. На каждую требуется затратить [math]n \cdot |P_A|[/math] операций, где [math]|P_A|[/math] – количество правил. Суммируя по всем правилам получаем конечную сложность [math]O \left( n^3 \cdot |\Gamma| \right)[/math].

Алгоритму требуется [math]n^2 \cdot |N|[/math] памяти, где [math]|N|[/math] – количество нетерминалов грамматики.

Минус алгоритма заключается в том, что изначально грамматику необходимо привести к НФХ.