Задача о выводе в контекстно-свободной грамматике, алгоритм Кока-Янгера-Касами — различия между версиями
Efimenko (обсуждение | вклад) (→Алгоритм Кока-Янгера-Касами) |
Lis (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
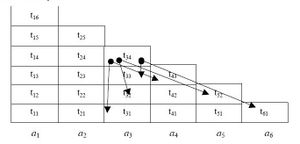
[[Файл:table.jpg|300px|thumb|right|Таблица разбора алгоритма для цепочки из шести символов. В клетку <tex>t_{34}</tex> должны быть помещены нетерминалы, из которых выводится фрагмент входной строки длиной четыре символа, начинающийся с <tex>a_{3}</tex>, т.е. это цепочка <tex>a_{3}a_{4}a_{5}a_{6}</tex>. Этот фрагмент тремя способами можно разбить на пары непустых соседних фрагментов: (1) <tex>a_{3}</tex> и <tex>a_{4}a_{5}a_{6}</tex>, (2): <tex>a_{3}a_{4}</tex> и <tex>a_{5}a_{6}</tex>, (3): <tex>a_{3}a_{4}a_{5}</tex> и <tex>a_{6}</tex>. Этим трем парам фрагментов соответствуют пары клеток, в которых могут стоять нетерминалы, из которых эти фрагменты выводятся: (1) <tex>t_{31}</tex> и <tex>t_{43}</tex>, (2): <tex>t_{32}</tex> и <tex>t_{52}</tex>, (3): <tex>t_{33}</tex> и <tex>t_{61}</tex>. Если в этих клетках находятся соответственно нетерминалы B и C и существует правило A→BC, то A заносится в <tex>t_{34}</tex>]] | [[Файл:table.jpg|300px|thumb|right|Таблица разбора алгоритма для цепочки из шести символов. В клетку <tex>t_{34}</tex> должны быть помещены нетерминалы, из которых выводится фрагмент входной строки длиной четыре символа, начинающийся с <tex>a_{3}</tex>, т.е. это цепочка <tex>a_{3}a_{4}a_{5}a_{6}</tex>. Этот фрагмент тремя способами можно разбить на пары непустых соседних фрагментов: (1) <tex>a_{3}</tex> и <tex>a_{4}a_{5}a_{6}</tex>, (2): <tex>a_{3}a_{4}</tex> и <tex>a_{5}a_{6}</tex>, (3): <tex>a_{3}a_{4}a_{5}</tex> и <tex>a_{6}</tex>. Этим трем парам фрагментов соответствуют пары клеток, в которых могут стоять нетерминалы, из которых эти фрагменты выводятся: (1) <tex>t_{31}</tex> и <tex>t_{43}</tex>, (2): <tex>t_{32}</tex> и <tex>t_{52}</tex>, (3): <tex>t_{33}</tex> и <tex>t_{61}</tex>. Если в этих клетках находятся соответственно нетерминалы B и C и существует правило A→BC, то A заносится в <tex>t_{34}</tex>]] | ||
| + | |||
| + | = Формальная грамматика = | ||
| + | |||
| + | '''Формальная грамматика''' - способ описания формального языка, то есть некоторого подмножества слов данного конечного алфавита. Выделяют ''порождающие'' грамматики, состоящие из следующих компонентов: | ||
| + | |||
| + | * 1) Множество '''терминальных символов''' ('''терминалов''') - символов алфавита, слова над которым определяет грамматика, то есть символов, непосредственно присутствующих в словах языка. | ||
| + | * 2) Множество '''нетерминальных символов''' ('''нетерминалов''') - объектов, выражающих некоторые структурные части языка, не имеющие конкретного представления как слова над алфавитом (таких, как формула или часть программы). | ||
| + | * 3) Множество '''правил вывода''' ('''продукций''') - правил вида L → R, где: | ||
| + | ** L - непустая последовательность терминальных и нетерминальных символов, содержищий по крайней мере один нетерминал. | ||
| + | ** R - любая (возможно, пустая) последовательность терминальных и нетерминальных символов. | ||
| + | * 4) S - стартовый нетерминал. | ||
| + | |||
| + | '''Выводом''' называется последовательность строк из терминалов и нетерминалов, такая, что: | ||
| + | * Первая строка состоит из стартового нетерминала | ||
| + | * Каждая следующая строка получена из предыдущей путем замена некоторой подстроки по некоторому правилу | ||
| + | * Последняя строка состоит только из терминалов (и, следовательно, не может быть преобразована по правилу грамматики). | ||
| + | |||
| + | Существование в грамматике вывода для получения конкретного слова - критерий принадлежности слова языку, определяемому грамматикой. | ||
| + | |||
| + | === Пример === | ||
| + | |||
| + | Терминалы: a, b. Нетерминалы: S, A, B. Продукции: | ||
| + | * S → AB | ||
| + | * A → AB | ||
| + | * AB → ba | ||
| + | * A → a | ||
| + | * B → b | ||
| + | |||
| + | Слова, выводимые в данной грамматике: ab, ba, abb, bab, abbb, babb, ... | ||
| + | |||
| + | Слова, невыводимые в данной грамматике: a, b, baa, baba, ... | ||
| + | |||
= Контекстно-свободная грамматика = | = Контекстно-свободная грамматика = | ||
| − | Контекстно-свободная грамматика (КС-грамматика, бесконтекстная грамматика) — частный случай формальной грамматики, у которой левые части всех правил являются одиночными нетерминалами. | + | '''Контекстно-свободная грамматика''' ('''КС-грамматика''', '''бесконтекстная грамматика''') — частный случай формальной грамматики, у которой левые части всех правил являются одиночными нетерминалами, то есть все её продукции имеют вид L → R, где L - нетерминал, а R - последовательность терминалов и нетерминалов. |
| − | + | ||
| − | * | + | === Пример === |
| − | + | ||
| − | + | Терминалы: (, ). Нетерминалы: S. Продукции: | |
| − | * | + | * S → SS |
| − | + | * S → () | |
| − | * | + | * S → (S) |
| − | + | ||
| − | + | Очевидно, что данная грамматика задает язык правильных скобочных последовательностей. Например, последовательность (()(())) может быть выведена следующим образом: | |
| − | + | * S → (S) → (SS) → (()(S)) → (()(())) | |
| − | |||
| − | = | + | = Нормальная форма Хомского = |
| − | + | '''Нормальная форма Хомского''' - нормальная форма КС-грамматик, в которой все продукции имеют вид: | |
| − | * | + | * A → a, где ''A'' - нетерминал, а ''a'' - терминал |
| − | * | + | * A → BC, где ''A'', ''B'', ''C'' - нетерминалы, причем ''B'' и ''C'' не являются начальными нетерминалами |
| − | * S → | + | * S → ε, где S - начальный нетерминал и ε - пустая строка (данная продукция необходима, если в языке присуствует пустая строка) |
| − | |||
| − | |||
| − | |||
| − | + | Покажем, что любую КС-грамматику можно привести к нормальной форме Хомского. Рассмотрим продукцию этой грамматики: <tex>A \Rightarrow A_1 A_2 A_3 ... A_n</tex>, где <tex>A_i</tex> - терминалы или нетерминалы. Добавим к грамматике нетерминалы <tex>B_1 ... B_n</tex>, <tex>C_k</tex> для таких k, что <tex>A_k</tex> - нетерминал, и продукции вида | |
| − | + | * <tex>A \Rightarrow B_1</tex> | |
| − | + | * <tex>B_i \Rightarrow A_i B_{i+1}</tex> если <tex>A_i</tex> - нетерминал | |
| + | * <tex>B_i \Rightarrow C_i B_{i+1}</tex> и <tex>C_i \Rightarrow A_i</tex>, если <tex>A_i</tex> - терминал | ||
= Алгоритм Кока-Янгера-Касами = | = Алгоритм Кока-Янгера-Касами = | ||
| − | Алгоритм | + | '''Алгоритм Кока-Янгера-Касами''' (''Cocke — Younger — Kasami algorithm'', '''CYK - алгоритм''') - универсальный алгоритм, позволяющий по слову узнать, выводимо ли оно в заданной КС-грамматике в нормальной форме Хомского. |
| + | |||
| + | Пусть дана строка <tex>a_1 a_2 ... a_n</tex>. Заведем трехмерный массив d, состоящий из логических значений, и <tex>d[A][i,j] = true</tex> тогда и только тогда, когда из нетерминала <tex>A</tex> правилами грамматики можно вывести подстроку <tex>a_i a_{i+1} ... a_j</tex>. Тогда: | ||
| + | * <tex>d[A][i,i] = true</tex>, если в грамматике присутствует правило <tex>A \Rightarrow a_i</tex>, иначе <tex>false</tex> | ||
| + | * Остальные элементы массива заполняются динамически: <tex>d[A][i,j] = \bigvee\limits_{A \Rightarrow BC}\bigvee\limits_{k = i}^{j-1} d[B][i,k] \wedge d[C][k+1,j]</tex>. То есть, подстроку <tex>a_i...a_j</tex> можно вывести из нетерминала <tex>A</tex>, если существует продукция <tex>A \Rightarrow BC</tex> и такое <tex>k</tex>, что подстрока <tex>a_i...a_k</tex> выводима из <tex>B</tex>, а подстрока <tex>a_{k+1}...a_j</tex> - из <tex>C</tex>. | ||
| + | |||
| + | Значение <tex>d[S][1,n]</tex> содержит ответ на вопрос, выводима ли данная строка в данной грамматике. | ||
| + | |||
| + | Очевидно, что алгоритм работает за время <tex>O(n^3)</tex> (где <tex>n</tex> - длина строки) и требует <tex>O(n^2)</tex> памяти (обе оценки с точностью до константных множителей, зависящих от конкретной грамматики). | ||
| + | |||
| + | Заметим, что если массив будет хранить целые числа, а формулу динамики заменить на <tex>d[A][i,j] = \sum\limits_{A \Rightarrow BC}\sum\limits_{k = i}^{j-1} d[B][i,k] \cdot d[C][k+1,j]</tex>, то <tex>d[A][i,j]</tex> - количество способов получить подстроку <tex>a_i...a_j</tex> из нетерминала <tex>A</tex>. | ||
| − | + | Пусть <tex>P_{A \Rightarrow BC}</tex> - ''стоимость'' вывода по правилу <tex>A \Rightarrow BC</tex>. Тогда, если использовать формулу <tex>d[A][i,j] = \min\limits_{A \Rightarrow BC} \min\limits_{k = i}^{j-1} ( d[B][i,k] + d[C][k+1,j] + P_{A \Rightarrow BC} )</tex>, то <tex>d[A][i,j]</tex> - минимальная стоимость вывода подстроки <tex>a_i...a_j</tex> из нетерминала <tex>A</tex>. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Таким образом, задача о выводе в КС-грамматике в нормальной форме Хомского является обобщением задачи динамического программирования на подотрезке. | |
| − | = | + | = Ссылки = |
* [http://www.intuit.ru/department/algorithms/mathformlang/7/] | * [http://www.intuit.ru/department/algorithms/mathformlang/7/] | ||
* [http://en.wikipedia.org/wiki/CYK_algorithm Википедия - CYK algorithm] | * [http://en.wikipedia.org/wiki/CYK_algorithm Википедия - CYK algorithm] | ||
* [http://www.ctc.msiu.ru/program/t-system/diploma/node39.html Алгоритм Кока-Янгера-Касами] | * [http://www.ctc.msiu.ru/program/t-system/diploma/node39.html Алгоритм Кока-Янгера-Касами] | ||
Версия 06:49, 6 декабря 2011
Содержание
Формальная грамматика
Формальная грамматика - способ описания формального языка, то есть некоторого подмножества слов данного конечного алфавита. Выделяют порождающие грамматики, состоящие из следующих компонентов:
- 1) Множество терминальных символов (терминалов) - символов алфавита, слова над которым определяет грамматика, то есть символов, непосредственно присутствующих в словах языка.
- 2) Множество нетерминальных символов (нетерминалов) - объектов, выражающих некоторые структурные части языка, не имеющие конкретного представления как слова над алфавитом (таких, как формула или часть программы).
- 3) Множество правил вывода (продукций) - правил вида L → R, где:
- L - непустая последовательность терминальных и нетерминальных символов, содержищий по крайней мере один нетерминал.
- R - любая (возможно, пустая) последовательность терминальных и нетерминальных символов.
- 4) S - стартовый нетерминал.
Выводом называется последовательность строк из терминалов и нетерминалов, такая, что:
- Первая строка состоит из стартового нетерминала
- Каждая следующая строка получена из предыдущей путем замена некоторой подстроки по некоторому правилу
- Последняя строка состоит только из терминалов (и, следовательно, не может быть преобразована по правилу грамматики).
Существование в грамматике вывода для получения конкретного слова - критерий принадлежности слова языку, определяемому грамматикой.
Пример
Терминалы: a, b. Нетерминалы: S, A, B. Продукции:
- S → AB
- A → AB
- AB → ba
- A → a
- B → b
Слова, выводимые в данной грамматике: ab, ba, abb, bab, abbb, babb, ...
Слова, невыводимые в данной грамматике: a, b, baa, baba, ...
Контекстно-свободная грамматика
Контекстно-свободная грамматика (КС-грамматика, бесконтекстная грамматика) — частный случай формальной грамматики, у которой левые части всех правил являются одиночными нетерминалами, то есть все её продукции имеют вид L → R, где L - нетерминал, а R - последовательность терминалов и нетерминалов.
Пример
Терминалы: (, ). Нетерминалы: S. Продукции:
- S → SS
- S → ()
- S → (S)
Очевидно, что данная грамматика задает язык правильных скобочных последовательностей. Например, последовательность (()(())) может быть выведена следующим образом:
- S → (S) → (SS) → (()(S)) → (()(()))
Нормальная форма Хомского
Нормальная форма Хомского - нормальная форма КС-грамматик, в которой все продукции имеют вид:
- A → a, где A - нетерминал, а a - терминал
- A → BC, где A, B, C - нетерминалы, причем B и C не являются начальными нетерминалами
- S → ε, где S - начальный нетерминал и ε - пустая строка (данная продукция необходима, если в языке присуствует пустая строка)
Покажем, что любую КС-грамматику можно привести к нормальной форме Хомского. Рассмотрим продукцию этой грамматики: , где - терминалы или нетерминалы. Добавим к грамматике нетерминалы , для таких k, что - нетерминал, и продукции вида
- если - нетерминал
- и , если - терминал
Алгоритм Кока-Янгера-Касами
Алгоритм Кока-Янгера-Касами (Cocke — Younger — Kasami algorithm, CYK - алгоритм) - универсальный алгоритм, позволяющий по слову узнать, выводимо ли оно в заданной КС-грамматике в нормальной форме Хомского.
Пусть дана строка . Заведем трехмерный массив d, состоящий из логических значений, и тогда и только тогда, когда из нетерминала правилами грамматики можно вывести подстроку . Тогда:
- , если в грамматике присутствует правило , иначе
- Остальные элементы массива заполняются динамически: . То есть, подстроку можно вывести из нетерминала , если существует продукция и такое , что подстрока выводима из , а подстрока - из .
Значение содержит ответ на вопрос, выводима ли данная строка в данной грамматике.
Очевидно, что алгоритм работает за время (где - длина строки) и требует памяти (обе оценки с точностью до константных множителей, зависящих от конкретной грамматики).
Заметим, что если массив будет хранить целые числа, а формулу динамики заменить на , то - количество способов получить подстроку из нетерминала .
Пусть - стоимость вывода по правилу . Тогда, если использовать формулу , то - минимальная стоимость вывода подстроки из нетерминала .
Таким образом, задача о выводе в КС-грамматике в нормальной форме Хомского является обобщением задачи динамического программирования на подотрезке.