Алгоритм масштабирования потока

Определение:

Алгоритм масштабирования потока — алгоритм поиска максимального потока путём регулирования пропускной способности рёбер. Этот алгоритм работает в предположении, что все пропускные способности рёбер целые, так как они легко представимы в двоичном виде.

Идея

Идея алгоритма в нахождении путей с высокой пропускной способностью в первую очередь, чтобы сразу сильно увеличивать поток по ним, а затем по всем остальным.

Пусть дан граф [math] G [/math] с целыми пропускными способностями: [math] \forall(u, v) \in EG \colon c(u,v) \in \mathbb{Z_+} [/math]. [math] U = \max\limits_{(u, v) \in EG} c(u, v) [/math] — максимальная пропускная способность. Запишем пропускную способность каждого ребра в двоичном виде. Тогда каждое число будет занимать [math] \lfloor \log_2 U \rfloor + 1 = n + 1 [/math] бит.

[math] c(u, v) = \sum\limits_{i = 0}^n a_i(u, v) \times 2^n, a_i(u, v) \in \{0, 1\} [/math]

Методом Форда-Фалкерсона находим поток [math] f_0 [/math] для графа [math] G_0 [/math] с урезанными пропускными способностями [math] c_0(u, v) = a_n(u, v) [/math]. Добавим следующий бит и находим следующее приближение для графа [math] G_1 [/math] с новыми пропускными способностями [math] c_1(u, v) = 2 a_n(u, v) + a_{n - 1}(u, v) - 2 f_0(u, v) [/math].

После [math] n + 1 [/math] итерации получим ответ к задаче.

Оценка сложности

Утверждение:

Время работы алгоритма — [math] O(E^2 \log U) [/math].

[math]\triangleright[/math]

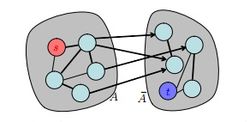
Количество итераций — [math] O(\log U) [/math]. Докажем, что сложность каждой итерации — [math] O(E^2) [/math]. На первом шаге ребра имеют пропускную способность [math] 1 [/math]. Значит, [math] |f_0| \leq |VG| [/math]. Поиск каждого дополнительного пути требует [math] O(E) [/math] времени, а их количество не больше [math] V [/math]. Итоговая сложность первой итерации — [math] O(VE) \leq O(E^2) [/math]. Разрез [math] (A, \overline{A}) [/math]. Докажем оценку для второго шага (для остальных доказательство аналогично). Граф [math] G_{f_0} [/math] — несвязен. Пусть [math] A [/math] — компонента связности, [math] s \in A, t \in \overline{A} [/math]. Тогда [math] c_{0_{f_0}}(A, \overline{A}) = 0 [/math]. Значит в графе с пропускными способностями [math] c_1 [/math]: [math] \forall u \in A, v \in \overline{A} \colon c_1(u, v) \leq 1 [/math].

[math]\triangleleft[/math]

Псевдокод

Capacity-Scaling
    [math] f \leftarrow 0 [/math]
    [math] \Delta \leftarrow 2^{\lfloor \log_2 U \rfloor}[/math]
    while [math] \Delta \gt 0[/math]
        do while в [math]G_f[/math] существует [math]s-t[/math] путь с пропускной способностью большей [math]\Delta[/math]
               do [math]P\leftarrow[/math] путь с пропускной способностью большей [math]\Delta[/math]
                  [math]\delta\leftarrow\min\{c_{ij}\colon(i,j)\in P\}[/math]
                  увеличить поток по рёбрам [math]P[/math] на [math]\delta[/math]
                  обновить [math]G_f[/math]
                  [math]f\leftarrow f+\delta[/math]
           [math]\Delta\leftarrow\Delta/2[/math]

Литература

• Olivier Juan, Yuri Boikov: Capacity Scaling for Graph Cuts in Vision
• Algorithm Tutorials. Maximum Flow: Augmenting Path Algorithms Comparison
• Андрей Станкевич: Задача о максимальном потоке