Поток минимальной стоимости — различия между версиями
Proshev (обсуждение | вклад) |
Proshev (обсуждение | вклад) |
||
| Строка 15: | Строка 15: | ||
== Задача о назначениях == | == Задача о назначениях == | ||
| − | [[Файл:Assignment.jpg|thumb| | + | [[Файл:Assignment.jpg|thumb|right|Задача о назначениях]] |
Условие: | Условие: | ||
* Дана квадратная матрица <tex>A_{N\times N}</tex>. Нужно выбрать в ней <tex>N</tex> элементов так, чтобы в каждой строке и в каждом столбце был выбран только один элемент, а сумма значений этих элементов была наименьшей. | * Дана квадратная матрица <tex>A_{N\times N}</tex>. Нужно выбрать в ней <tex>N</tex> элементов так, чтобы в каждой строке и в каждом столбце был выбран только один элемент, а сумма значений этих элементов была наименьшей. | ||
Версия 08:03, 27 декабря 2011
Определение задачи
Задача о потоке минимальной стоимости состоит в нахождении самого дешёвого способа передачи определённого количества потока через заданную сеть.
| Определение: |
| Дано число и транспортная сеть с источником и стоком , где ребра имеют пропускную способность и цену .
Суть задачи — найти поток f(u, v):
|
Алгоритмы решения
- Найти любой поток величины , после чего избавиться от всех циклов отрицательной стоимости в остаточном графе. Чтобы избавиться от цикла, надо пустить по нему максимально возможный поток. Циклы ищутся алгоритмом Форда - Беллмана.
- Поиск потока минимальной стоимости методом дополнения вдоль путей минимальной стоимости.
- Использование потенциалов Джонсона при поиске потока минимальной стоимости (модификация предыдущего алгоритма).
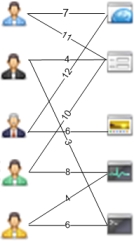
Задача о назначениях
Условие:
- Дана квадратная матрица . Нужно выбрать в ней элементов так, чтобы в каждой строке и в каждом столбце был выбран только один элемент, а сумма значений этих элементов была наименьшей.
- Имеется заказов и станков. Про каждый заказ известна стоимость его изготовления на каждом станке. На каждом станке можно выполнять только один заказ. Требуется распределить все заказы по станкам так, чтобы минимизировать суммарную стоимость.
Решение данной задачи легко сводится к поиску потока минимальной стоимости.
Источник
- Кормен, Томас Х., Лейзерсон, Чарльз И., Ривест, Рональд Л., Штайн Клиффорд Алгоритмы: построение и анализ, 2-е издание. Пер. с англ. — М.:Издательский дом "Вильямс", 2010. — 1296 с.: ил. — Парал. тит. англ. — ISBN 978-5-8459-0857-5 (рус.)