Стековые машины, эквивалентность двухстековой машины МТ — различия между версиями
Воронов (обсуждение | вклад) |
Воронов (обсуждение | вклад) |
||
| Строка 20: | Строка 20: | ||
|proof= | |proof= | ||
Для упрощения доказательства без умаления общности предположим, что вход для двухстековой машины заканчивается специальным символом <tex>\$</tex>, которого нет в исходном алфавите (аналог пробела в МТ). <br> | Для упрощения доказательства без умаления общности предположим, что вход для двухстековой машины заканчивается специальным символом <tex>\$</tex>, которого нет в исходном алфавите (аналог пробела в МТ). <br> | ||
| + | [[Изображение:SM.png|400px|thumb|left|Рис. 2. Представление ленты МТ двумя стеками]] | ||
<tex>\Rightarrow)</tex> | <tex>\Rightarrow)</tex> | ||
Докажем, что если язык <tex>L</tex> допускается машиной Тьюринга, то он допускается двухстековой машиной. <br> | Докажем, что если язык <tex>L</tex> допускается машиной Тьюринга, то он допускается двухстековой машиной. <br> | ||
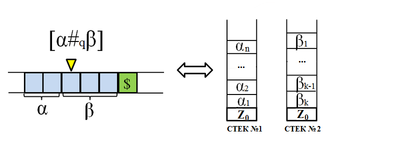
| − | + | Мы будем имитировать ленту МТ двумя стеками (Рис. 2). В первом стеке будет хранится кусок ленты слева от положения головки, во втором стеке — справа, включая текущий. Разумеется, куски ленты хранятся без бесконечных цепочек пробелов, окружающих значащие символы ленты. <br> | |
| − | Мы будем имитировать ленту МТ двумя стеками ( | ||
Исходя из необходимости инициализировать стеки для того, чтобы их содержимое корректно отражало содержимое ленты МТ, строящаяся нами двухстековая машина сначала читает весь вход до конца (он помечен маркером <tex>\$</tex>) и кладёт каждый новый поступивший символ на первый стек. Затем наша машина перебрасывает все значения из первого стека во второй, таким образом получив пустой первый стек (что соответствует бесконечной цепочке пробелов слева от головки МТ) и второй стек, содержащий весь вход (что соответствует положению всех значащих символов ленты МТ не левее от головки МТ). После этого машина перейдёт в начальное (имитируемое) состояние МТ. <br> | Исходя из необходимости инициализировать стеки для того, чтобы их содержимое корректно отражало содержимое ленты МТ, строящаяся нами двухстековая машина сначала читает весь вход до конца (он помечен маркером <tex>\$</tex>) и кладёт каждый новый поступивший символ на первый стек. Затем наша машина перебрасывает все значения из первого стека во второй, таким образом получив пустой первый стек (что соответствует бесконечной цепочке пробелов слева от головки МТ) и второй стек, содержащий весь вход (что соответствует положению всех значащих символов ленты МТ не левее от головки МТ). После этого машина перейдёт в начальное (имитируемое) состояние МТ. <br> | ||
| − | Теперь в каждый момент имитации мы будем знать прочтённый головкой символ | + | Теперь в каждый момент имитации мы будем знать текущий прочтённый головкой символ (им является вершина второго стека), и, соответственно, переход в МТ. <br> |
| + | Действие "<tex>\leftarrow</tex>" МТ (сдвинуть головку влево) будем имитировать простым перекидыванием вершины первого стека на второй. Стоит обратить внимание на случай, когда первый стек перед действием был пуст, что говорило бы нам о том, что слева от головки бесконечная цепочка из пробелов. Поэтому такой переход имитировался добавлением на второй стек символа пробела и оставлением первого стека пустым. Аналогично делаются "сдвинуть головку вправо" и "остаться на месте". После имитации действия соответствующего перехода в МТ, двухстековая машина делает переход в имитируемое новое состояние МТ. <br> | ||
| + | Допускающими состояниями двухстековой машины являются те, которые имитируют допускающие состояния МТ. <br> | ||
| + | Таким образом, мы с помощью двухстековой машины сымитировали МТ. | ||
| − | <tex>\Leftarrow)</tex> | + | [[Изображение:SMM.png|400px|thumb|left|Рис. 3. Представление двух стеков лентой МТ]] |
| + | <tex>\Leftarrow)</tex> Докажем, что если язык <tex>L</tex> допускается двухстековой машиной, то он допускается машиной Тьюринга. <br> | ||
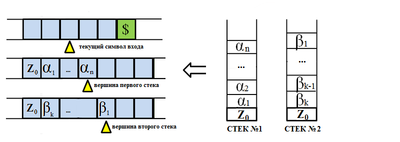
| + | Двухстековую машину можно сымитировать трехленточной МТ (Рис. 3). На первой ленте будет записан вход, вторая лента будет имитировать первый стек, третья — второй. <br> | ||
| + | Стеки имитируются Конечный автомат для МТ получим из двухстековой машины следующей заменой действия на переходе: | ||
}} | }} | ||
Версия 13:20, 28 декабря 2011
Стековая машина
Стековая машина является обобщением детерминированных МП-автоматов использованием нескольких стеков вместо одного.
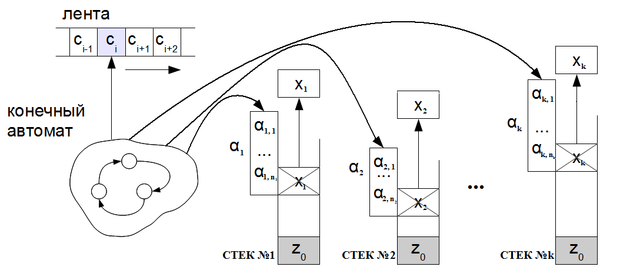
На рис. 1 изображена k-стековая машина. С ленты последовательно считываются символы входного алфавита ( — текущий считываемый символ). Для каждого стека с вершины снимается символ , вместо него помещается строка таким образом, чтобы первый символ строки находился на вершине стека и делается переход в автомате в зависимости от считанного с ленты символа и снятых со стеков верхних значений .
| Определение: |
-cтековой машиной называется набор A=, где
|
Эквивалентность двухстековой машины машине Тьюринга
| Теорема: |
Язык допускается машиной Тьюринга тогда и только тогда, когда он допускается двухстековой машиной. |
| Доказательство: |
|
Для упрощения доказательства без умаления общности предположим, что вход для двухстековой машины заканчивается специальным символом , которого нет в исходном алфавите (аналог пробела в МТ).
Докажем, что если язык допускается машиной Тьюринга, то он допускается двухстековой машиной. Докажем, что если язык допускается двухстековой машиной, то он допускается машиной Тьюринга. |