Стековые машины, эквивалентность двухстековой машины МТ — различия между версиями
Воронов (обсуждение | вклад) |
Воронов (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
== Стековая машина == | == Стековая машина == | ||
| − | [[Изображение:PDAk.png|620px|thumb|left|Рис. 1. | + | [[Изображение:PDAk.png|620px|thumb|left|Рис. 1. k-стековая машина]] |
Стековая машина является обобщением детерминированных МП-автоматов использованием нескольких стеков вместо одного. <br> | Стековая машина является обобщением детерминированных МП-автоматов использованием нескольких стеков вместо одного. <br> | ||
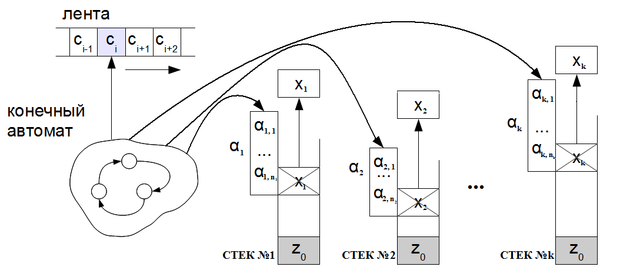
На рис. 1 изображена '''k-стековая машина'''. С ленты последовательно считываются символы входного алфавита (<tex>c_i</tex> — текущий считываемый символ). Для каждого стека с вершины снимается символ <tex>x_i</tex>, вместо него помещается строка <tex>\alpha_i</tex> таким образом, чтобы первый символ строки находился на вершине стека и делается переход в автомате в зависимости от считанного с ленты символа <tex>c_i</tex> и снятых со стеков верхних значений <tex>x_i</tex>. | На рис. 1 изображена '''k-стековая машина'''. С ленты последовательно считываются символы входного алфавита (<tex>c_i</tex> — текущий считываемый символ). Для каждого стека с вершины снимается символ <tex>x_i</tex>, вместо него помещается строка <tex>\alpha_i</tex> таким образом, чтобы первый символ строки находился на вершине стека и делается переход в автомате в зависимости от считанного с ленты символа <tex>c_i</tex> и снятых со стеков верхних значений <tex>x_i</tex>. | ||
Версия 20:23, 28 декабря 2011
Стековая машина
Стековая машина является обобщением детерминированных МП-автоматов использованием нескольких стеков вместо одного.
На рис. 1 изображена k-стековая машина. С ленты последовательно считываются символы входного алфавита ( — текущий считываемый символ). Для каждого стека с вершины снимается символ , вместо него помещается строка таким образом, чтобы первый символ строки находился на вершине стека и делается переход в автомате в зависимости от считанного с ленты символа и снятых со стеков верхних значений .
| Определение: |
-cтековой машиной называется набор A=, где
|
Эквивалентность двухстековой машины машине Тьюринга
| Теорема: |
Язык допускается машиной Тьюринга тогда и только тогда, когда он допускается двухстековой машиной. |
| Доказательство: |
|
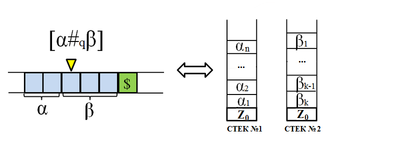
Для упрощения доказательства без умаления общности предположим, что вход для двухстековой машины заканчивается специальным символом , которого нет в исходном алфавите.
Докажем, что если язык допускается машиной Тьюринга, то он допускается двухстековой машиной. |