Алгоритм Куна для поиска максимального паросочетания — различия между версиями
| Строка 11: | Строка 11: | ||
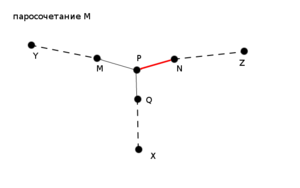
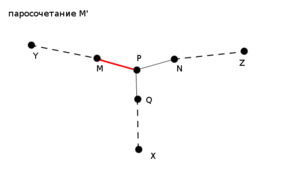
: Пусть <tex>p</tex> - ближайшая к <tex>x</tex> вершина, которая принадлежит и новой дополняющей цепи и цепи <tex>(y \rightsquigarrow z)</tex>. | : Пусть <tex>p</tex> - ближайшая к <tex>x</tex> вершина, которая принадлежит и новой дополняющей цепи и цепи <tex>(y \rightsquigarrow z)</tex>. | ||
: Тогда <tex>MP</tex> - последнее ребро на отрезке <tex>(y \rightsquigarrow p)</tex> цепи <tex>(y \rightsquigarrow z)</tex>, <tex>NP</tex> - последнее ребро на отрезке <tex>(z \rightsquigarrow p)</tex> цепи <tex>(y \rightsquigarrow z)</tex>, <tex>QP</tex> - последнее ребро лежащее на отрезке <tex>(x \rightsquigarrow p)</tex> новой дополняющей цепи(см. Рисунок 1).<br><br> | : Тогда <tex>MP</tex> - последнее ребро на отрезке <tex>(y \rightsquigarrow p)</tex> цепи <tex>(y \rightsquigarrow z)</tex>, <tex>NP</tex> - последнее ребро на отрезке <tex>(z \rightsquigarrow p)</tex> цепи <tex>(y \rightsquigarrow z)</tex>, <tex>QP</tex> - последнее ребро лежащее на отрезке <tex>(x \rightsquigarrow p)</tex> новой дополняющей цепи(см. Рисунок 1).<br><br> | ||
| − | : Допустим <tex>MP</tex> принадлежит паросочетанию <tex>M'</tex>, тогда <tex>NP</tex> ему не принадлежит.<br><br> | + | : Допустим <tex>MP(NP)</tex> принадлежит паросочетанию <tex>M'</tex>, тогда <tex>NP(MP)</tex> ему не принадлежит.<br><br> |
| − | : Поскольку паросочетание <tex>M'</tex> получается из <tex>M</tex> изменением вдоль дополняющей цепи <tex>(y \rightsquigarrow z)</tex>, в паросочетание <tex>M</tex> входило ребро <tex>NP</tex>, а ребро <tex>MP</tex> нет. | + | : Поскольку паросочетание <tex>M'</tex> получается из <tex>M</tex> изменением вдоль дополняющей цепи <tex>(y \rightsquigarrow z)</tex>, в паросочетание <tex>M</tex> входило ребро <tex>NP(MP)</tex>, а ребро <tex>MP(NP)</tex> нет. |
: Кроме того, ребро <tex>QP</tex> не лежит ни в исходном паросочетании <tex>M</tex>, ни в паросочетании <tex>M'</tex>, в противном случае оказалось бы, что вершина <tex>p</tex> инцидентна нескольким ребрам из паросочетания, что противоречит определению паросочетания.<br><br> | : Кроме того, ребро <tex>QP</tex> не лежит ни в исходном паросочетании <tex>M</tex>, ни в паросочетании <tex>M'</tex>, в противном случае оказалось бы, что вершина <tex>p</tex> инцидентна нескольким ребрам из паросочетания, что противоречит определению паросочетания.<br><br> | ||
:Тогда заметим, что цепь <tex>(x \rightsquigarrow z)</tex>, полученная объединением цепей <tex>(x \rightsquigarrow p)</tex> и <tex>(p \rightsquigarrow z)</tex>, по определению будет дополняющей в паросочетании <tex>M</tex>, что приводит к противоречию, поскольку в паросочетании <tex>M</tex> из вершины <tex>x</tex> не существует дополняющей цепи. | :Тогда заметим, что цепь <tex>(x \rightsquigarrow z)</tex>, полученная объединением цепей <tex>(x \rightsquigarrow p)</tex> и <tex>(p \rightsquigarrow z)</tex>, по определению будет дополняющей в паросочетании <tex>M</tex>, что приводит к противоречию, поскольку в паросочетании <tex>M</tex> из вершины <tex>x</tex> не существует дополняющей цепи. | ||
| Строка 18: | Строка 18: | ||
==Алгоритм== | ==Алгоритм== | ||
| − | |||
| − | |||
:Алгоритм просматривает все вершины графа по очереди, запуская из каждой обход (в глубину или в ширину), пытающийся найти увеличивающую цепь, начинающуюся в этой вершине. | :Алгоритм просматривает все вершины графа по очереди, запуская из каждой обход (в глубину или в ширину), пытающийся найти увеличивающую цепь, начинающуюся в этой вершине. | ||
:Краткое описание алгоритма: | :Краткое описание алгоритма: | ||
:* Возьмём пустое паросочетание | :* Возьмём пустое паросочетание | ||
| − | :* | + | :* Разобьем граф на две доли |
| − | :* Повторяем процесс поиска увеличивающей цепи | + | :* Проходя по всем вершинам первой доли пытаемся найти увеличивающую цепь |
| − | + | :* Если удается найти увеличивающую цепь, выполняем чередование паросочетания вдоль этой цепи | |
| − | :* Найденное паросочетание и является максимальным | + | :* Повторяем процесс поиска увеличивающей цепи |
| + | :* Найденное паросочетание и является максимальным | ||
| Строка 38: | Строка 37: | ||
:Рассмотрим поиск увеличивающей цепи обходом в глубину. | :Рассмотрим поиск увеличивающей цепи обходом в глубину. | ||
:* Изначально обход в глубину стоит в текущей ненасыщенной вершине <tex>v</tex> первой доли. | :* Изначально обход в глубину стоит в текущей ненасыщенной вершине <tex>v</tex> первой доли. | ||
| − | :* Просматриваем все рёбра из этой вершины, пусть текущее ребро — <tex>(v, | + | :* Просматриваем все рёбра из этой вершины, пусть текущее ребро — <tex>(v, to)</tex>. |
| − | :* Если вершина | + | :* Если вершина <tex>to</tex> ещё не насыщена паросочетанием, то, значит, мы смогли найти увеличивающую цепь: она состоит из единственного ребра <tex>(v, to)</tex>. |
:** Включаем это ребро в паросочетание и прекращаем поиск увеличивающей цепи из вершины <tex>v</tex>. | :** Включаем это ребро в паросочетание и прекращаем поиск увеличивающей цепи из вершины <tex>v</tex>. | ||
| − | : | + | :* Иначе, — если уже насыщена каким-то ребром <tex>(p, to)</tex> и не посещена, то попытаемся пройти вдоль этого ребра: тем самым мы попробуем найти увеличивающую цепь, проходящую через рёбра <tex>(v, t_0), (t_0, p)</tex>. Для этого просто перейдем в нашем обходе в вершину <tex>p</tex>. |
| − | : | + | :** Пробуем найти увеличивающую цепь из вершины <tex>p</tex>. |
: Этот обход, запущенный из вершины <tex>v</tex>, либо найдёт увеличивающую цепь, и тем самым насытит вершину, либо же такой увеличивающей цепи не найдёт (и, следовательно, эта вершина уже не сможет стать насыщенной). | : Этот обход, запущенный из вершины <tex>v</tex>, либо найдёт увеличивающую цепь, и тем самым насытит вершину, либо же такой увеличивающей цепи не найдёт (и, следовательно, эта вершина уже не сможет стать насыщенной). | ||
| Строка 48: | Строка 47: | ||
: После того, как все вершины <tex>v = 1 ... n_1</tex> будут просмотрены, текущее паросочетание будет максимальным. | : После того, как все вершины <tex>v = 1 ... n_1</tex> будут просмотрены, текущее паросочетание будет максимальным. | ||
| + | : Корректность алгоритма следует из [[Теорема о максимальном паросочетании и дополняющих цепях|теоремы Бержа]] и теоремы, описанной выше.<br> | ||
==Релизация== | ==Релизация== | ||
| Строка 90: | Строка 90: | ||
==Время работы== | ==Время работы== | ||
| − | :Итак, алгоритм Куна можно представить как серию из | + | :Итак, алгоритм Куна можно представить как серию из <tex>n_1</tex> запусков обхода в глубину на всём графе. |
| − | :Следовательно, всего этот алгоритм исполняется за время <tex>O( | + | :Следовательно, всего этот алгоритм исполняется за время <tex>O(nm)</tex>, где <tex>m</tex> - количество ребер, что в худшем случае есть <tex>O(n^3)</tex>. |
| + | |||
| + | |||
| + | :Более точная оценка: | ||
| + | :В описанной выше реализации запуски обхода в глубину/ширину происходят только из вершин первой доли, поэтому весь алгоритм исполняется за время <tex>O(n_1)</tex> , где <tex>n_1</tex> — число вершин первой доли. В худшем случае это составляет <tex>O(n_1^2n_2)</tex>, (где <tex>n_2</tex> — число вершин второй доли). | ||
==Источники== | ==Источники== | ||
Версия 22:02, 8 января 2012
Содержание
Теорема
| Теорема: |
Если из вершины не существует дополняющей цепи относительно паросочетания и паросочетание получается из изменением вдоль дополняющей цепи, тогда из не существует дополняющей цепи в . |
| Доказательство: |
|
Алгоритм
- Алгоритм просматривает все вершины графа по очереди, запуская из каждой обход (в глубину или в ширину), пытающийся найти увеличивающую цепь, начинающуюся в этой вершине.
- Краткое описание алгоритма:
- Возьмём пустое паросочетание
- Разобьем граф на две доли
- Проходя по всем вершинам первой доли пытаемся найти увеличивающую цепь
- Если удается найти увеличивающую цепь, выполняем чередование паросочетания вдоль этой цепи
- Повторяем процесс поиска увеличивающей цепи
- Найденное паросочетание и является максимальным
- Будем считать, что граф уже разбит на две доли.
- Просматриваем все вершины первой доли графа :
- Если текущая вершина уже насыщена текущим паросочетанием (т.е. уже выбрано какое-то смежное ей ребро), то эту вершину пропускаем
- Иначе — алгоритм пытается насытить эту вершину, для чего запускается поиск увеличивающей цепи, начинающейся с этой вершины.
- Рассмотрим поиск увеличивающей цепи обходом в глубину.
- Изначально обход в глубину стоит в текущей ненасыщенной вершине первой доли.
- Просматриваем все рёбра из этой вершины, пусть текущее ребро — .
- Если вершина ещё не насыщена паросочетанием, то, значит, мы смогли найти увеличивающую цепь: она состоит из единственного ребра .
- Включаем это ребро в паросочетание и прекращаем поиск увеличивающей цепи из вершины .
- Иначе, — если уже насыщена каким-то ребром и не посещена, то попытаемся пройти вдоль этого ребра: тем самым мы попробуем найти увеличивающую цепь, проходящую через рёбра . Для этого просто перейдем в нашем обходе в вершину .
- Пробуем найти увеличивающую цепь из вершины .
- Этот обход, запущенный из вершины , либо найдёт увеличивающую цепь, и тем самым насытит вершину, либо же такой увеличивающей цепи не найдёт (и, следовательно, эта вершина уже не сможет стать насыщенной).
- После того, как все вершины будут просмотрены, текущее паросочетание будет максимальным.
- Корректность алгоритма следует из теоремы Бержа и теоремы, описанной выше.
Релизация
- Граф хранится списками смежности
- Функция - обход в глубину, возвращает если есть увеличивающая цепь из вершины .
- В массиве хранятся паросочетания. Паросочетание есть ребро .
bool dfs(int v)
{
if (used[v])
return false;
used[v] = true;
for (int i = 0; i < g[v].size(); i++)
{
int to = g[v][i];
if (mt[to] == -1 || dfs(mt[to]))
{
mt[to] = v;
return true;
}
}
return false;
}
int main()
{
... чтение графа ...
mt.assign (k, -1);
for (int v = 0; v < n; v++)
{
used.assign(n, false);
dfs(v);
}
for (int i = 0; i < k; i++)
if (mt[i] != -1)
... вывод ...
}
Время работы
- Итак, алгоритм Куна можно представить как серию из запусков обхода в глубину на всём графе.
- Следовательно, всего этот алгоритм исполняется за время , где - количество ребер, что в худшем случае есть .
- Более точная оценка:
- В описанной выше реализации запуски обхода в глубину/ширину происходят только из вершин первой доли, поэтому весь алгоритм исполняется за время , где — число вершин первой доли. В худшем случае это составляет , (где — число вершин второй доли).
Источники
- MAXimal :: algo :: Алгоритм Куна нахождения наибольшего паросочетания
- Асанов М., Баранский В., Расин В. - Дискретная математика: Графы, матроиды, алгоритмы — СПб.: Издательство "Лань", 2010. — 291 стр.