Действие перестановки на набор из элементов, представление в виде циклов — различия между версиями

Материал из Викиконспекты
Перейти к: навигация, поиск
Строка 1: Строка 1:
−
'''Перестановка''' — это отображение <tex>\pi:X\rightarrow X</tex>, которое каждому <tex>x_i \in X</tex> ставит во взаимно-однозначное соответствие <tex>x_j \in X</tex>
+
== Действие перестановки на набор элементов ==
−
[[Файл:cycles.gif|150px|right|thumb|Изображение перестановки в виде графа]]
+
 
 +
{{Определение
 +
|definition=
 +
Пусть <tex>\pi</tex> {{---}} перестановка порядка <tex>n</tex>, и <tex>\{a_i\}</tex> {{---}} множество некоторых объектов, занумерованных числами от одного до <tex>n</tex>. Тогда результатом действия перестановки на этот набор объектов назовём множество объектов <tex>\{b_i\}</tex>, занумерованных числами от одного до <tex>n</tex>, причём <tex>b_i = a_{\pi_i}</tex>.
 +
}}
 +
 
 +
Обозначим за <tex>A</tex> множество (не пронумерованных) объектов <tex>\{a_1, \dots, a_n\}</tex>. Поскольку перестановку можно рассматривать как отображение <tex>\pi \colon \{1, \dots, n\} \to \{1, \dots, n\}</tex>, а нумерацию как отображение <tex>\alpha \colon \{1, \dots, n\} \to A</tex>, то действие перестановки можно определить как композицию отображений <tex>\alpha \circ \pi</tex>.
 +
 
 +
Например, рассмотрим множество <tex>A = (a, b, c, d)</tex> и перестановку <tex>\pi = \langle 3, 4, 1, 2 \rangle</tex>. Тогда результат действия <tex>\pi</tex> на <tex>A</tex> {{---}} упорядоченное множество <tex>\pi(A) = (c, d, a, b)</tex>.
  
 +
Также, композицию перестановок можно выразить как действие одной перестановки на другую.
  
−
Индексы <tex>i,j \in \mathcal{f}1, 2, \ldots, n\mathcal{g}</tex>, где <tex>n = \mathcal{j}X\mathcal{j}</tex>.
 
−
Число <tex>~n</tex> называют порядком перестановки. Перестановку можно записать в виде упорядоченного набора из чисел <tex>1, 2,\ldots, n</tex>.
 
−
Элемент такого набора <tex>~\mathcal{h}a_1,a_2,\ldots,a_n\mathcal{i}~ a_k</tex> означает, что <tex>~\pi (x_{a_k}) = x_k </tex>. Таким образом, если <tex> \Theta = \mathcal{h}x_1,x_{2},\ldots,x_{n}\mathcal{i}</tex> — упорядоченный набор элементов из множества<tex>~X</tex>, то <tex>\pi (\Theta) = \mathcal{h}x_{q_1},x_{q_2},\ldots,x_{q_n}\mathcal{i} </tex>, где <tex>q_{a_i} = i</tex>. Например, применив перестановку <tex>~\mathcal{h}3,2,4,1\mathcal{i}</tex> к набору элементов <tex>~(x_1,x_2,x_3,x_4)</tex>, получим набор <tex>~\mathcal{h}x_4,x_2,x_1,x_3\mathcal{i}</tex>. <br\>
 
−
==Произведение перестановок==
 
−
Произведением перестановок <tex>~\pi</tex> и <tex>~\sigma</tex> называется композиция (т.е. последовательное применение) этих перестановок: <tex>(\pi*\sigma)(\Theta) = \pi(\sigma(\Theta)) = \pi \circ \sigma (\Theta)</tex>.
 
−
Легко показать, что произведение перестановок тоже является перестановкой, причем если <tex>~\phi = \pi*\sigma</tex>, то <tex>\phi(x_i) = \pi \circ \sigma (x_i)</tex>.
 
 
==Циклы==
 
==Циклы==
−
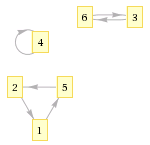
Циклом длины <tex>~l</tex> называется такая перестановка <tex>~\pi,</tex> которая тождественна на всём множестве <tex>X,</tex> кроме подмножества <tex>\{x_1,x_2,\dots,x_l\}\subset X</tex> и <tex>~\pi(x_l)=x_1,</tex> <tex>~\pi(x_i)=x_{i+1}.</tex> Обозначается <tex>(x_1,x_2,\dots,x_l).</tex> Перестановку также можно записать в виде произведения непересекающихся циклов, причём единственным образом с точностью до порядка следования циклов в произведении. Например: <tex>~(1, 5, 2)(3, 6)(4)=\mathcal{h}5,1,6,4,2,3\mathcal{i} </tex>.  
+
[[Файл:cycles.gif|150px|right|thumb|Изображение перестановки в виде графа]]
 +
Циклом длины <tex>~l</tex> называется такая перестановка <tex>\pi,</tex> которая тождественна на всём множестве <tex>X,</tex> кроме подмножества <tex>\{x_1,x_2,\dots,x_l\}\subset X</tex> и <tex>\pi(x_l)=x_1</tex>, <tex>\pi(x_i)=x_{i+1}.</tex> Обозначается <tex>(x_1,x_2,\dots,x_l)</tex>. Перестановку можно записать в виде произведения непересекающихся циклов, причём единственным образом с точностью до порядка следования циклов в произведении. Например: <tex>(1, 5, 2)(3, 6)(4)=\langle 5,1,6,4,2,3\rangle </tex>.  
  
−
Перестановку можно представить в виде графа. Граф содержит ребро от вершины <tex>~x_i</tex> к вершине <tex>~x_j</tex> если <tex>~\pi(x_j) = x_i</tex>, то есть элемент <tex>~x_i</tex> переходит в <tex>~x_j</tex> после применения перестановки <tex>~\pi</tex>. Тогда циклы перестановки соответствуют циклическим путям в графе.
+
Перестановку можно представить в виде графа. Граф содержит ребро от вершины <tex>x_i</tex> к вершине <tex>x_j</tex> если <tex>\pi(x_i) = x_j</tex>. Тогда циклы перестановки соответствуют циклическим путям в графе.

Версия 11:46, 12 января 2012

Действие перестановки на набор элементов

Определение:
Пусть [math]\pi[/math] — перестановка порядка [math]n[/math], и [math]\{a_i\}[/math] — множество некоторых объектов, занумерованных числами от одного до [math]n[/math]. Тогда результатом действия перестановки на этот набор объектов назовём множество объектов [math]\{b_i\}[/math], занумерованных числами от одного до [math]n[/math], причём [math]b_i = a_{\pi_i}[/math].


Обозначим за [math]A[/math] множество (не пронумерованных) объектов [math]\{a_1, \dots, a_n\}[/math]. Поскольку перестановку можно рассматривать как отображение [math]\pi \colon \{1, \dots, n\} \to \{1, \dots, n\}[/math], а нумерацию как отображение [math]\alpha \colon \{1, \dots, n\} \to A[/math], то действие перестановки можно определить как композицию отображений [math]\alpha \circ \pi[/math].

Например, рассмотрим множество [math]A = (a, b, c, d)[/math] и перестановку [math]\pi = \langle 3, 4, 1, 2 \rangle[/math]. Тогда результат действия [math]\pi[/math] на [math]A[/math] — упорядоченное множество [math]\pi(A) = (c, d, a, b)[/math].

Также, композицию перестановок можно выразить как действие одной перестановки на другую.

Циклы

Изображение перестановки в виде графа

Циклом длины [math]~l[/math] называется такая перестановка [math]\pi,[/math] которая тождественна на всём множестве [math]X,[/math] кроме подмножества [math]\{x_1,x_2,\dots,x_l\}\subset X[/math] и [math]\pi(x_l)=x_1[/math], [math]\pi(x_i)=x_{i+1}.[/math] Обозначается [math](x_1,x_2,\dots,x_l)[/math]. Перестановку можно записать в виде произведения непересекающихся циклов, причём единственным образом с точностью до порядка следования циклов в произведении. Например: [math](1, 5, 2)(3, 6)(4)=\langle 5,1,6,4,2,3\rangle [/math].

Перестановку можно представить в виде графа. Граф содержит ребро от вершины [math]x_i[/math] к вершине [math]x_j[/math] если [math]\pi(x_i) = x_j[/math]. Тогда циклы перестановки соответствуют циклическим путям в графе.

Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Действие_перестановки_на_набор_из_элементов,_представление_в_виде_циклов&oldid=16264»