Каскадный сумматор — различия между версиями
Sementry (обсуждение | вклад) м (поправил пунктуацию) |
|||
| Строка 1: | Строка 1: | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | '''Каскадный сумматор''' {{---}} логическая [[Реализация булевой функции схемой из функциональных элементов| | + | '''Каскадный сумматор''' {{---}} логическая [[Реализация булевой функции схемой из функциональных элементов|схема]], осуществляющая сложение многоразрядных двоичных чисел. |
}} | }} | ||
| − | Как известно, с помощью [[Сумматор|полного сумматора]] можно сложить 2 одноразрядных двоичных числа. Для сложения двух | + | Как известно, с помощью [[Сумматор|полного сумматора]] можно сложить 2 одноразрядных двоичных числа. Для сложения двух <tex>n</tex>-разрядных двоичных чисел можно использовать <tex>n</tex> полных сумматоров. |
| − | |||
| − | + | При сложении двух чисел в <tex>i</tex>-том разряде складываются <TeX>a_i</TeX>, <Tex>b_i</TeX> и входной бит переноса (carry-in bit) <TeX>c_i</TeX>. Младший разряд суммы записывается в <tex>i</tex>-й разряд ответа (<TeX>s_i</TeX>), а старший становится выходным битом переноса (carry-out bit) <TeX>c_{i+1}</TeX> и используется при сложении в следующем разряде. | |
| + | |||
| + | При этом в первый входной бит переноса подаётся ноль, а последний бит переноса даёт старший разряд суммы. | ||
| + | |||
| + | Прежде чем сложить <tex>i</tex>-ые биты, надо ждать выходного бита переноса от сложения <tex> i-1 </tex> битов, то есть сумма в каждом разряде может зависеть от суммы предыдущих разрядов. Поэтому сложение с помощью каскадного сумматора выполняется за время <tex>O(n)</tex>. | ||
Версия 12:03, 12 января 2012
| Определение: |
| Каскадный сумматор — логическая схема, осуществляющая сложение многоразрядных двоичных чисел. |
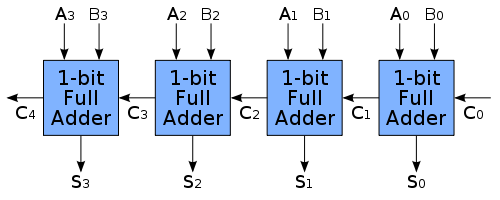
Как известно, с помощью полного сумматора можно сложить 2 одноразрядных двоичных числа. Для сложения двух -разрядных двоичных чисел можно использовать полных сумматоров.
При сложении двух чисел в -том разряде складываются , и входной бит переноса (carry-in bit) . Младший разряд суммы записывается в -й разряд ответа (), а старший становится выходным битом переноса (carry-out bit) и используется при сложении в следующем разряде.
При этом в первый входной бит переноса подаётся ноль, а последний бит переноса даёт старший разряд суммы.
Прежде чем сложить -ые биты, надо ждать выходного бита переноса от сложения битов, то есть сумма в каждом разряде может зависеть от суммы предыдущих разрядов. Поэтому сложение с помощью каскадного сумматора выполняется за время .