Полином Жегалкина — различия между версиями
(→Метод треугольника) |
(→Преобразование Мёбиуса) |
||
| Строка 205: | Строка 205: | ||
Любая булева функция представима в виде полинома Жегалкина, притом единственным образом. | Любая булева функция представима в виде полинома Жегалкина, притом единственным образом. | ||
| − | Пусть <tex> i = ( | + | Пусть <tex> i = (i_1, i_2, .. i_n), \;\; i_k \in \{0 ; 1\}</tex>, и введем обозначение <tex> x ^{i_k} \sim \left\{\begin{matrix} x, \;\; i_k=1 |
\\ 1, \;\; i_k=0 | \\ 1, \;\; i_k=0 | ||
\end{matrix}\right. </tex> . | \end{matrix}\right. </tex> . | ||
| Строка 212: | Строка 212: | ||
<tex> f(x) = \bigoplus\limits_i \alpha_i \cdot x_1^{i_1} \cdot x_2^{i_2} \cdot ... \cdot x_n^{i_n}</tex>, где <tex>\alpha_i \in \{ 0; 1 \}</tex>. | <tex> f(x) = \bigoplus\limits_i \alpha_i \cdot x_1^{i_1} \cdot x_2^{i_2} \cdot ... \cdot x_n^{i_n}</tex>, где <tex>\alpha_i \in \{ 0; 1 \}</tex>. | ||
| − | Множество коэффициентов <tex>\{\alpha _i\}</tex> можно рассматривать как функцию <tex>\alpha</tex>, заданной на множестве индексов <tex> i | + | Множество коэффициентов <tex>\{\alpha _i\}</tex> можно рассматривать как функцию <tex>\alpha</tex>, заданной на множестве индексов <tex> i = (i_1, i_2, .. i_n)</tex>, то есть <tex>\alpha: i \mapsto \alpha_i</tex>. |
Очевидно, функцию <tex> f </tex> можно записать и следующим образом: <tex> f(x) = \bigoplus \limits_i \alpha_i \cdot [x_1 , \; </tex> если <tex> \;\; i_1] \cdot [x_2 , \; </tex> если <tex> \;\; i_2] \cdot ... \cdot [x_n , \; </tex> если <tex> \;\; i_n]</tex>. | Очевидно, функцию <tex> f </tex> можно записать и следующим образом: <tex> f(x) = \bigoplus \limits_i \alpha_i \cdot [x_1 , \; </tex> если <tex> \;\; i_1] \cdot [x_2 , \; </tex> если <tex> \;\; i_2] \cdot ... \cdot [x_n , \; </tex> если <tex> \;\; i_n]</tex>. | ||
| Строка 218: | Строка 218: | ||
Тут запись <tex>[x_k , \; </tex> если <tex> \; i_k]</tex> означает, что элелемент <tex> x_k </tex> присутствует в соответствующем члене полинома только если <tex> i_k = 1 </tex>. | Тут запись <tex>[x_k , \; </tex> если <tex> \; i_k]</tex> означает, что элелемент <tex> x_k </tex> присутствует в соответствующем члене полинома только если <tex> i_k = 1 </tex>. | ||
Тогда если для какого-то <tex>x</tex>, <tex>i \succ x</tex> ,то в слагаемом будет существовать хотя бы один множитель, равный нулю, и такое слагаемое на сумму не повлияет. | Тогда если для какого-то <tex>x</tex>, <tex>i \succ x</tex> ,то в слагаемом будет существовать хотя бы один множитель, равный нулю, и такое слагаемое на сумму не повлияет. | ||
| − | Отсюда ясно, что <tex> f(x) = \bigoplus \limits_{i \preceq x} \alpha_i </tex>. <tex> (2) </tex> | + | Отсюда ясно, что |
| + | |||
| + | <tex> f(x) = \bigoplus \limits_{i \preceq x} \alpha_i </tex>. <tex> (2) </tex> | ||
| + | |||
Найдем отображение <tex> f \mapsto \alpha</tex> (То есть такое, которое по заданной функции вычисляет значения всех коэффициентов). | Найдем отображение <tex> f \mapsto \alpha</tex> (То есть такое, которое по заданной функции вычисляет значения всех коэффициентов). | ||
{{Теорема | {{Теорема | ||
| − | |statement=Пусть задана функция <tex> f </tex>. Тогда функцию <tex> \alpha_x </tex> можно найти по формуле: <tex>\alpha_x = \bigoplus \limits_{j\preceq x} f(j)</tex> <tex> (3) </tex>. | + | |statement=Пусть задана функция <tex> f </tex>. Тогда функцию <tex> \alpha_x </tex> можно найти по формуле: <tex>\alpha_x = \bigoplus \limits_{j\preceq x} f(j)</tex> <tex> (3) </tex>. |
||proof=Докажем при помощи индукции по количеству единиц в векторе <tex> x </tex> ( иначе говоря, по сумме <tex>x_1+x_2+...+x_n</tex> ) и для удобства обозначим это количество единиц(сумму) <tex> wt(x) </tex>. | ||proof=Докажем при помощи индукции по количеству единиц в векторе <tex> x </tex> ( иначе говоря, по сумме <tex>x_1+x_2+...+x_n</tex> ) и для удобства обозначим это количество единиц(сумму) <tex> wt(x) </tex>. | ||
Версия 16:24, 13 января 2012
Полином Жегалкина — полином с коэффициентами вида 0 и 1, где в качестве произведения берётся конъюнкция, а в качестве сложения исключающее или. Полином был предложен в 1927 году И. И. Жегалкиным в качестве удобного средства для представления функций булевой логики. Полином Жегалкина имеет следующий вид:
Содержание
Предпосылки
По теореме Поста, чтобы система булевых функций была полной, надо, чтобы в ней существовали
- Хотя бы одна функция, не сохраняющая 0;
- Хотя бы одна функция, не сохраняющая 1;
- Хотя бы одна нелинейная функция;
- Хотя бы одна немонотонная функция;
- Хотя бы одна несамодвойственная функция.
Исходя из этого, система функций является полной, так как в ней:
- Не сохраняет 0: ;
- Не сохраняет 1: ;
- Нелинейна: ;
- Немонотонна: ;
- Несамодвойственны: .
На основе этой системы и строятся полиномы Жегалкина.
Построение полинома Жегалкина
Существует несколько способов построения полинома Жегалкина.
По таблице истинности
Пусть для функции задана таблица истинности. Запишем сначала данную функцию в виде полинома Жегалкина с неопределёнными коэффициентами. Затем по очереди подставляем всевозможные наборы в порядке увеличения количества единиц и находим коэффициенты с учётом того, что , а . За каждую подстановку находим только один коэффициент.
Пример: Дана функция и её таблица истинности:
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 |
Построим для неё полином Жегалкина:
Так как , то . Далее подставляем все остальные наборы в порядке возрастания числа единиц, подставляя вновь полученные значения в следующие формулы:
Таким образом, полином Жегалкина выглядит так:
Преобразование дизъюнктивной нормальной формы
Этот способ основан на том, что . Если функция задана в виде ДНФ, то можно сначала убрать дизъюнкцию, используя правило Де-Моргана, а все отрицания заменить прибавлением единицы по модулю два, после чего раскрыть скобки по обычным правилам, при этом учитывая, что четное число одинаковых слагаемых равно нулю (так как ), а нечетное число одинаковых слагаемых равно одному такому слагаемому. Либо же можно заменить дизъюнкцию по следующему правилу:
.
Если функция задана в СДНФ, то так как при любых значениях входных переменных в единицу обращается не более одного члена выражения, то достаточно просто заменить все дизъюнкции исключающим ИЛИ.
Пример: Дана функция в ДНФ , построим полином Жегалкина.
Запишем функцию так:
;
Сгруппируем слагаемые и воспользуемся преобразованием (1):
Воспользуемся свойствами конъюнкции и , а также тем, что , и упростим выражение:
Ещё раз воспользуемся преобразованием (1):
Раскроем скобку по алгебраическим правилам:
Снова воспользуемся свойствами конъюнкции и исключающего ИЛИ:
Заменим отрицание на прибавление :
Раскроем скобки:
Выкинем парные слагаемые и получим окончательную формулу:
Метод треугольника
Метод треугольника позволяет преобразовать таблицу истинности в полином Жегалкина путём построения вспомогательной треугольной таблицы в соответствии со следующими правилами:
- Строится полная таблица истинности, в которой строки идут в порядке возрастания двоичных кодов от 000...00 до 111...11.
- Строится вспомогательная треугольная таблица, в которой первый столбец совпадает со столбцом значений функции в таблице истинности.
- Ячейка в каждом последующем столбце получается путём сложения по модулю 2 двух ячеек предыдущего столбца — стоящей в той же строке и строкой ниже.
- Столбцы вспомогательной таблицы нумеруются двоичными кодами в том же порядке, что и строки таблицы истинности.
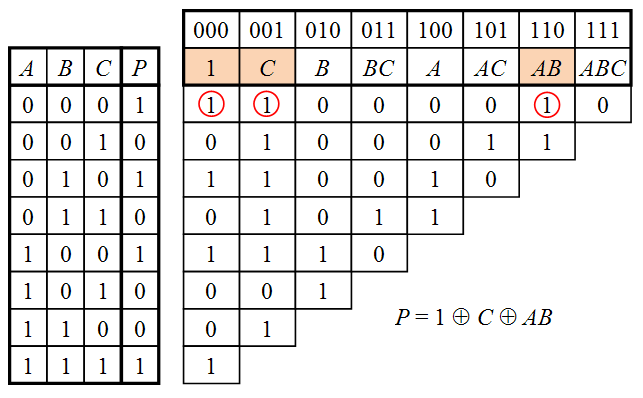
- Каждому двоичному коду ставится в соответствие один из членов полинома Жегалкина в зависимости от позиций кода, в которых стоят единицы. Например, ячейке 111 соответствует член ABC, ячейке 101 — член AC, ячейке 010 — член B, ячейке 000 — член 1 и т.д.
- Если в верхней строке какого-либо столбца стоит единица, то соответствующий член присутствует в полиноме Жегалкина.
Фактически, этот метод является модификацией метода построения по таблице истинности, описанного выше. По сравнению с ним он удобнее тем, что расчёты занимают мало места и в них сложнее ошибиться, но метод треугольника требует бо́льшего количества операций.
Пример преобразования таблицы истинности в полином Жегалкина для функции трёх переменных P(A,B,C) показан на рисунке.
Чтобы получить формулу, по которой рассчитывается какой-либо коэффициент, нужно из клетки, в которой он записан, пройтись всеми возможными путями влево, до столбца P таблицы истинности, делая ходы влево и влево-вниз, записать значения в конечных ячейках и сложить их все между собой по модулю 2.
Таким образом, в первом столбце сверху записан коэффициент ,
во втором — ,
в третьем — ,
в четвёртом —
и так далее, то есть при построении вспомогательной таблицы коэффициенты полинома просчитываются автоматически.
Преобразование Мёбиуса
Пусть задана булева функция . Любая булева функция представима в виде полинома Жегалкина, притом единственным образом.
Пусть , и введем обозначение .
Тогда полином Жегалкина можно записать как: , где .
Множество коэффициентов можно рассматривать как функцию , заданной на множестве индексов , то есть .
Очевидно, функцию можно записать и следующим образом: если если если .
Тут запись если означает, что элелемент присутствует в соответствующем члене полинома только если . Тогда если для какого-то , ,то в слагаемом будет существовать хотя бы один множитель, равный нулю, и такое слагаемое на сумму не повлияет. Отсюда ясно, что
.
Найдем отображение (То есть такое, которое по заданной функции вычисляет значения всех коэффициентов).
| Теорема: |
Пусть задана функция . Тогда функцию можно найти по формуле: . |
| Доказательство: |
|
Докажем при помощи индукции по количеству единиц в векторе ( иначе говоря, по сумме ) и для удобства обозначим это количество единиц(сумму) . 1) База: если , то, очевидно 2) Пускай теорема справедлива для всех сумм . Покажем, что в таком случае она верна и для . По , а далее по предположению индукции видим: . Рассмотрим сумму . Каждый элемент содержится в ней, только если , и для фиксированных элемент встречается ровно столько раз, сколько существует , таких, что . Несложно увидеть, что таких существует ровно , то есть нечетное количество раз. Тогда . Но тогда . То есть при формула также выполняется, значит при любых выполняется . |
Отображение также называется преобразованием Мёбиуса.
Видно, что и — это одно и тоже преобразование. Значит, если применить преобразование Мёбиуса к функции, а затем вновь применить то же преобразование к получившейся функции, тогда вновь получим исходную функцию . То есть преобразование Мёбиуса обратно самому себе, иными словами, является инволюцией.
Литература и источники информации
- Cтатистика | Математика НГУ
- Википедия
- Е.Л Рабкин, Ю.Б. Фарфоровская, дискретная математика
- Логачёв О.А, Сальников А.А., Ященко В.В. Булевы фунции в теории кодирования и криптологии — МЦНМО, 2004. - 470с. — ISBN 5-94057-117-4.