Эргодическая марковская цепь

Определение:

Марковская цепь называется эргодической, если существует дискретное распределение (называемое эргодическим) [math]\pi = (\pi_1,\pi_2,\ldots )^{\top}[/math], такое что [math]\pi_i \gt 0,\; i \in \mathbb{N}[/math] и [math]\lim\limits_{n \to \infty} p_{ij}^{(n)} = \pi_j, \quad \forall i=1,2, \ldots[/math].

Эргодические цепи могут быть регулярными или циклическими. Циклические цепи отличаются от регулярных тем, что в процессе переходов через определенное количество шагов (цикл) происходит возврат в какое-либо состояние. Регулярные цепи этим свойством не обладают.

Стационарный режим

Эргодические марковские цепи описываются сильно связным графом. Это означает, что в такой системе возможен переход из любого состояния [math]S_i[/math] в любое состояние [math]S_{j}, (i,j = 1,2,...,n)[/math] за конечное число шагов.

Для эргодических цепей при достаточно большом времени функционирования ([math]t \to \infty[/math]) наступает стационарный режим, при котором вероятности [math]p_i[/math] состояний системы не зависят от времени и не зависят от распределения вероятностей в начальный момент времени, т.е. [math]p_i = const[/math].

Для определения стационарных вероятностей [math]p_i[/math] нахождения системы в состоянии [math]S_{i}[/math] нужно составить систему [math]n[/math] линейных однородных алгебраических уравнений с [math]n[/math] неизвестными:

[math]p_{i} = \sum\limits_{j=1}^{n}(p_{j} \times p_{ji})[/math], где [math]i = 1,2,...,n ~~~~~~~~ (1)[/math]

Причем, искомые вероятности должны удовлетворять условию:

[math]\sum\limits_{j=1}^{n}(p_{i}) = 1 ~~~~~~~~ (2)[/math]

Систему линейных алгебраических уравнений удобно составлять непосредственно по графу состояний. При этом в левой части уравнения записывается вероятность состояния, соответствующего рассматриваемой вершине графа, а в правой части - сумма произведений. Число слагаемых соответствует числу дуг графа, входящих в рассматриваемое состояние. Каждое слагаемое представляет произведение вероятности того состояния, из которого выходит дуга графа, на переходную вероятность, которой помечена соответствующая дуга графа.

Получается, для определения стационарных вероятностей нам нужно решить систему уравнений (1). Из которой у нас получится бесконечное количество решений. Проверяя полученные решения на выполнение уравнения (2) получим, что система имеет единственное решение.

Основная теорема об эргодических распределениях

Теорема (Основная теорема об эргодических распределениях):

Пусть [math]\{X_n\}_{n \ge 0}[/math] - цепь Маркова с дискретным пространством состояний и матрицей переходных вероятностей [math]P = (p_{ij}),\; i,j=1,2,\ldots[/math]. Тогда эта цепь является эргодической тогда и только тогда, когда она Неразложима (т.е. цепь Маркова такова, что её состояния образуют лишь один неразложимый класс ); Положительно возвратна (т.е. находится в таком состоянии, выйдя из которого возвращается в него за конечное время); Апериодична (т.е. находится в таком состоянии, которое навещается цепью через промежутки времени, не кратные фиксированному числу). Эргодическое распределение [math]\mathbf{\pi}[/math] тогда является единственным решением системы: [math]\sum\limits_{i=0}^{\infty} \pi_i = 1,\; \pi_j \ge 0,\; \pi_j = \sum\limits_{i=0}^{\infty} \pi_i\, p_{ij},\quad \, j\in \mathbb{N}[/math].

Пример

Пример эргодической цепи

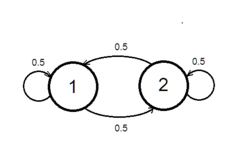
Рассмотрим эксперимент по бросанию честной монеты. Тогда соответствующая этому эксперименту марковская цепь будет иметь 2 состояния. Состояние меняется на противоположное, при бросании монеты, с вероятностью [math]p = 0.5[/math].

Рассмотрим матрицу, следующего вида: [math]p_{ij}=0.5, i,j=1,2[/math]. Такая матрица является стохастической, а, значит, корректно определяет марковскую цепь. Такая цепь является эргодической, так как существует эргодическое распределение [math]\pi = (0.5,0.5)^{\top}[/math], такое что [math]\lim\limits_{n \to \infty} p_{ij}^{(n)} = \pi_j, i=1,2[/math].

Ссылки

• Эргодическое распределение - Википедия

• Дискретное распределение - Википедия

Литература

Дж. Кемени, Дж. Снелл "Конечные цепи Маркова" - Издательство "Наука", 1970 г - 129 c.