Действие перестановки на набор из элементов, представление в виде циклов — различия между версиями
| Строка 5: | Строка 5: | ||
Пусть <tex>\pi</tex> {{---}} перестановка порядка <tex>n</tex>, и <tex>\{a_i\}</tex> {{---}} множество некоторых объектов, занумерованных числами от одного до <tex>n</tex>. Тогда результатом действия перестановки на этот набор объектов назовём множество объектов <tex>\{b_i\}</tex>, занумерованных числами от одного до <tex>n</tex>, причём <tex>b_i = a_{\pi_i}</tex>. | Пусть <tex>\pi</tex> {{---}} перестановка порядка <tex>n</tex>, и <tex>\{a_i\}</tex> {{---}} множество некоторых объектов, занумерованных числами от одного до <tex>n</tex>. Тогда результатом действия перестановки на этот набор объектов назовём множество объектов <tex>\{b_i\}</tex>, занумерованных числами от одного до <tex>n</tex>, причём <tex>b_i = a_{\pi_i}</tex>. | ||
}} | }} | ||
| + | |||
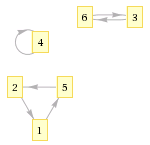
| + | [[Файл:Permutation_action.png|400px|thumb|right|Иллюстрация действия перестановки]] | ||
Обозначим за <tex>A</tex> множество (не пронумерованных) объектов <tex>\{a_1, \dots, a_n\}</tex>. Поскольку перестановку можно рассматривать как отображение <tex>\pi \colon \{1, \dots, n\} \to \{1, \dots, n\}</tex>, а нумерацию как отображение <tex>\alpha \colon \{1, \dots, n\} \to A</tex>, то действие перестановки можно определить как композицию отображений <tex>\alpha \circ \pi</tex>. | Обозначим за <tex>A</tex> множество (не пронумерованных) объектов <tex>\{a_1, \dots, a_n\}</tex>. Поскольку перестановку можно рассматривать как отображение <tex>\pi \colon \{1, \dots, n\} \to \{1, \dots, n\}</tex>, а нумерацию как отображение <tex>\alpha \colon \{1, \dots, n\} \to A</tex>, то действие перестановки можно определить как композицию отображений <tex>\alpha \circ \pi</tex>. | ||
| − | Например, рассмотрим множество <tex>A = (a, b, c, d)</tex> и перестановку <tex>\pi = \langle 3, 4, 1, 2 \rangle</tex>. Тогда результат действия <tex>\pi</tex> на <tex>A</tex> {{---}} упорядоченное множество <tex>\pi(A) = (c, d, a, b)</tex>. | + | Например, рассмотрим множество <tex>A = (a, b, c, d)</tex> и перестановку <tex>\pi = \langle 3, 4, 1, 2 \rangle</tex>. Тогда результат действия <tex>\pi</tex> на <tex>A</tex> {{---}} упорядоченное множество <tex>\pi(A) = (c, d, a, b)</tex>. Если рассмотреть граф перестановки (описано ниже), то действие перестановки можно представить таким образом: каждый элемент устанавливается в вершину графа, соответствующую номеру этого элемента, после чего каждый элемент передвигается по исходящему из этой вершины ребру. |
Также, композицию перестановок можно выразить как действие одной перестановки на другую. | Также, композицию перестановок можно выразить как действие одной перестановки на другую. | ||
Версия 14:18, 16 января 2012
Действие перестановки на набор элементов
| Определение: |
| Пусть — перестановка порядка , и — множество некоторых объектов, занумерованных числами от одного до . Тогда результатом действия перестановки на этот набор объектов назовём множество объектов , занумерованных числами от одного до , причём . |
Обозначим за множество (не пронумерованных) объектов . Поскольку перестановку можно рассматривать как отображение , а нумерацию как отображение , то действие перестановки можно определить как композицию отображений .
Например, рассмотрим множество и перестановку . Тогда результат действия на — упорядоченное множество . Если рассмотреть граф перестановки (описано ниже), то действие перестановки можно представить таким образом: каждый элемент устанавливается в вершину графа, соответствующую номеру этого элемента, после чего каждый элемент передвигается по исходящему из этой вершины ребру.
Также, композицию перестановок можно выразить как действие одной перестановки на другую.
Циклы
Циклом длины называется такая перестановка которая тождественна на всём множестве кроме подмножества и , Обозначается . Перестановку можно записать в виде произведения непересекающихся циклов, причём единственным образом с точностью до порядка следования циклов в произведении. Например: .
Перестановку можно представить в виде графа. Граф содержит ребро от вершины к вершине если . Тогда циклы перестановки соответствуют циклическим путям в графе.