Использование обхода в глубину для поиска компонент сильной связности — различия между версиями
(→Доказательство корректности алгоритма) |
Dimitrova (обсуждение | вклад) (→Алгоритм) |
||
| Строка 2: | Строка 2: | ||
[[Категория: Обход в глубину]] | [[Категория: Обход в глубину]] | ||
==Алгоритм== | ==Алгоритм== | ||
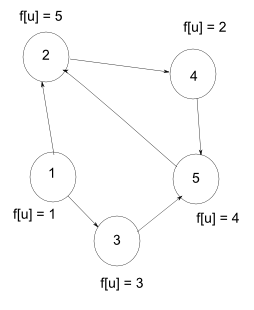
| + | [[Файл:Сильная_связность.png|300px|thumb| вершины 2, 4, 5 сильносвязаны]] | ||
[[Отношение_связности,_компоненты_связности#Сильная связность|Компоненты сильной связанности]] можно найти с помощью [[Обход_в_глубину,_цвета_вершин | поиска в глубину]] в 3 этапа: | [[Отношение_связности,_компоненты_связности#Сильная связность|Компоненты сильной связанности]] можно найти с помощью [[Обход_в_глубину,_цвета_вершин | поиска в глубину]] в 3 этапа: | ||
#Построить граф <tex>H</tex> с обратными (инвертированными) рёбрами | #Построить граф <tex>H</tex> с обратными (инвертированными) рёбрами | ||
Версия 23:35, 17 января 2012
Содержание
Алгоритм
Компоненты сильной связанности можно найти с помощью поиска в глубину в 3 этапа:
- Построить граф с обратными (инвертированными) рёбрами
- Выполнить в поиск в глубину и найти — время окончания обработки вершины
- Выполнить поиск в глубину в , перебирая вершины во внешнем цикле в порядке убывания
Полученные на 3-ем этапе деревья поиска в глубину будут являться компонентами сильной связности графа .
Так как компоненты сильной связности и графа совпадают, то первый поиск в глубину для нахождения можно выполнить на графе , а второй — на .
Доказательство корректности алгоритма
| Теорема: |
Вершины и взаимно достижимы после выполнения алгоритма они оказываются в одной компонентe сильной связанности. |
| Доказательство: |
|
Если вершины и были взаимно достижимы в графе , то во время выполнения третьего шага алгоритма обе вершины окажутся в одном поддереве по свойству обхода в глубину. Следовательно они будут находится в одной компоненте сильной связности.
1) Вершины и оказались в одной компоненте связности, т.е. принадлежат одному и тому же дереву поиска в глубину на третьем этапе алгоритма. Значит, что они обе достижимы из корня этого дерева. 2) Вершина была рассмотрена вторым обходом в глубину раньше, чем и , значит время выхода из нее при первом обходе в глубину больше, чем время выхода из вершин и . Из этого мы получаем 2 случая: а) Обе эти вершины были достижимы из в инвертированном графе. А это означает взаимную достижимость вершин и и взаимную достижимость вершин и . А складывая пути мы получаем взаимную достижимость вершин и . б) Между и этими вершинами вообще нет пути ни в одну сторону, ни в другую при первом обходе в инверитированном графе. Но последнего быть не может, так как эти вершины были достижимы из по пункту 1). Значит, из случая а) и не существования случая б) получаем, что вершины и взаимно достижимы в обоих графах. |
Время работы алгоритма
- Для того, чтобы инвертировать все ребра в графе, представленном в виде списка потребуется действий. Для матричного представления графа ненужно выполнять никакие действия для его инвертирования.
- Количество ребер в инвертированном равно количеству ребер в изначальном графе, поэтому поиск в глубину будет работать за
- Поиск в глубину в исходном графе выполняется за .
В итоге получаем, что время работы алгоритма .
Псевдокод
Пусть — исходный граф, —инвертированный граф. В массиве будем хранить номера вершин в порядке окончания обработки поиском в глубину в графе . В результате получаем массив , который каждой вершине сопоставляет номер её компоненты.
dfs1() for (всех смежных с ) if (вершина не посещена) dfs1() Добавляем вершину в конец списка dfs2() for (всех смежных с ) if (если вершина еще не находится ни в какой компоненте) dfs2() main() считываем исходные данные, формируем массивы и for (по всем вершинам графа ) if (вершина не посещена) dfs1(i) for (по всем вершинам списка в обратном порядке) if (если вершина не находится ни в какой компоненте) dfs2() ++
Литература
- Р.Седжвик. "Фундаментальные алгоритмы на С++. Алгоритмы на графах" - СПб, ДиаСофтЮП, 2002