Теорема о существовании простого цикла в случае существования цикла

Эта статья находится в разработке!

Теорема:

Если между двумя вершинами неориентированного графа существуют два различных рёберно-простых пути, то в этом графе существует простой цикл.

Доказательство:

[math]\triangleright[/math]

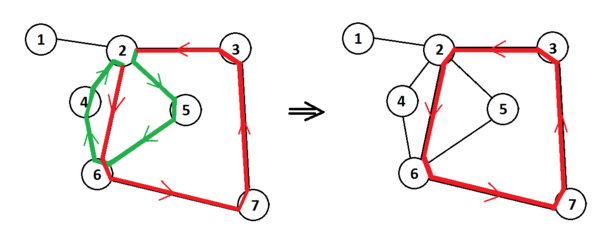
Возьмём два существующих пути между нужными нам вершинами: [math]V_0E_1V_1E_2V_2 ... E_nV_n[/math], [math]v_0e_1v_1e_2v_2 ... e_mv_m[/math], [math]V_0 = v_0[/math], [math]V_n = v_m[/math]. Удалим из путей одинаковые префиксы и суффиксы, оставив из тех только последние и первые вершины, соответственно. Оставшиеся пути: [math]V_aE_{a+1} ... E_bV_b[/math], [math]v_ae_{a+1} ... e_cv_c[/math], [math]V_a = v_a[/math], [math]V_b = v_c[/math], [math]E_{a+1} \neq e_{a+1}[/math], [math]E_b \neq e_c[/math]. Рассмотрим конкатенацию первого нового пути и развёрнутого второго нового пути. Она будет циклом, так как начальная и конечная вершины совпадают, изначально пути были рёберно-простыми, а в точке соединения, равно как и в точке замыкания цикла, условие различности двух идущих подряд рёбер выполняется. Мы получили цикл, определим его: [math]V_0E_1V_1 ... E_kV_k[/math], [math]V_0 = V_k[/math]. Алгоритм: 1. Для вершины [math]V_i[/math] найдём момент её последнего вхождения в цикл - [math]V_j[/math]. 2. Удалим отрезок цикла от [math]E_{i+1}[/math] до [math]V_j[/math], включительно. Получившаяся последовательность вершин и рёбер графа останется циклом, и в нём вершина [math]V_i[/math] будет содержаться ровно один раз. Начнём процесс с вершины [math]V_1[/math] и будем повторять его каждый раз для следующей вершины нового цикла, пока не дойдём до последней. По построению, получившийся цикл будет содержать каждую из вершин графа не более одного раза, а значит, будет простым.

[math]\triangleleft[/math]

Для вершины 2 находим последнее ее вхождение в цикл и удаляем отрезок цикла, выделенный зеленым.
[(2, 5) - 5 - (5, 6) - 6 - (6, 4) - 4 - (4, 2) - 2]

Лемма:

Наличие двух различных рёберно-простых путей между какими-либо двумя вершинами графа [math]G[/math] равносильно наличию цикла в этом графе.

Доказательство:

[math]\triangleright[/math]

"[math]\Rightarrow[/math]" Предположим, что в графе [math]G[/math] существует два различных реберно-простых пути между вершинами [math]u[/math] и [math]v[/math]. Пусть это будут пути [math]p = u e_1 v_1\ldots v_{n-1} e_n v[/math] и [math]p' = u e'_1 v'_1\ldots v'_{n-1} e'_n v[/math]. Пусть их наибольший общий префикс заканчивается в вершине [math]w = v_k = v'_l[/math]. Заметим, что [math]w \neq v[/math], т. к. пути различны. Рассмотрим суффиксы путей [math]p[/math] и [math]p'[/math]: [math]s = w e_{k+1} \ldots v[/math] и [math]s' = w e'_{l+1} \ldots v[/math] соответственно. Найдем первую совпадающую вершину [math]w'[/math] в [math]s[/math] и [math]s'[/math], не равную [math]w[/math]. Осталось заметить, что замкнутый путь [math]c[/math], полученный объединением [math]w \rightarrow w'[/math] части пути [math]s[/math] вместе с [math]w' \rightarrow w[/math] частью цепи [math]s'[/math] является циклическим путем. Действительно, т. r. в путях [math]s[/math] и [math]s'[/math] двух ребер подряд не бывает, т.к. это реберно простые пути, а ребра, смежные с [math]w[/math] и [math]w'[/math] не совпадают по построению. Циклический путь [math]c[/math] является представителем некоторого цикла в графе [math]G[/math]. "[math]\Leftarrow[/math]" Предположим, что в графе [math]G[/math] существует цикл и пусть циклический путь [math]c = v_0 e_1 v_1 \ldots e_n v_0[/math] — его представитель. Найдем первую точку [math]w = v_k = v_l (l \gt k)[/math] пересечения [math]c[/math] с самим собой. Необходимо такая точка существует, т.к. путь замкнутый. Рассмотрим циклический путь [math]v_k e_{k+1} \ldots e_l v_l[/math]: он простой, т. к. если это неверно и существует вершина [math]v_j = v_j' (k \lt j \lt j' \lt l)[/math], то в [math]c[/math] вершина [math]v_j'[/math] повторяется раньше, чем [math]v_l[/math]. Теперь элементарно взяв две вершины [math]v_k[/math] и [math]v_{k+1}[/math] легко заметить, что существует два различных реберно-неперсекающихся пути между ними: [math]v_k e_{k+1} v_{k+1}[/math] и [math]v_k e_l v_{l - 1} \ldots v_k[/math].

[math]\triangleleft[/math]

Замечания

• Так как вершинно-простой путь всегда является рёберно-простым, первая теорема справедлива и для вершинно-простых путей (усиление условия).
• Так как вершинно-простой цикл всегда является рёберно-простым, первая теорема справедлива и для рёберно-простого цикла (ослабление результата).
• Утверждение

Если две вершины графа лежат на цикле, то они лежат на простом цикле.

в общем случае неверно, так как эти вершины могут лежать в разных компонентах вершинной или рёберной двусвязности: все пути из одной вершины в другую будут содержать одну и ту же точку сочленения или один и тот же мост.

См. также

• Основные определения теории графов
• Теорема о существовании простого пути в случае существования пути
• Отношение реберной двусвязности
• Отношение вершинной двусвязности