Построение по НКА эквивалентного ДКА, алгоритм Томпсона — различия между версиями
Admin (обсуждение | вклад) |
|||
| Строка 40: | Строка 40: | ||
===Пример=== | ===Пример=== | ||
| − | Пусть нам дан [[Недетерминированные конечные автоматы|недетерменированный конечный автомат]]: [[Файл:DKA. | + | Пусть нам дан [[Недетерминированные конечные автоматы|недетерменированный конечный автомат]]: [[Файл:DKA.png]] |
По нашему заданию эквивалентного ДКА мы получаем: [[Файл:NKA_definition.png]] | По нашему заданию эквивалентного ДКА мы получаем: [[Файл:NKA_definition.png]] | ||
| Строка 46: | Строка 46: | ||
#Помещаем в очередь множество из одной стартовой вершины — <tex>\{1\}</tex>: <tex>Q = \{\{1\}\}</tex>. | #Помещаем в очередь множество из одной стартовой вершины — <tex>\{1\}</tex>: <tex>Q = \{\{1\}\}</tex>. | ||
#Достаём из очереди множество <tex>\{1\}</tex>: <tex>Q = \{\}</tex>. | #Достаём из очереди множество <tex>\{1\}</tex>: <tex>Q = \{\}</tex>. | ||
| − | #<tex>q_d(\{1\}, a) = \{1, 2\}</tex>, | + | #<tex>q_d(\{1\}, a) = \{1, 2\}</tex>, кладём множество <tex>\{1, 2\}</tex> в очередь: <tex>Q = \{\{1, 2\}\}</tex>. |
#<tex>q_d(\{1\}, b) = \{1\}</tex>, нам не надо класть множество <tex>\{1\}</tex> в очередь, так как оно уже там было. | #<tex>q_d(\{1\}, b) = \{1\}</tex>, нам не надо класть множество <tex>\{1\}</tex> в очередь, так как оно уже там было. | ||
#Достаём из очереди множество <tex>\{1, 2\}</tex>: <tex>Q = \{\}</tex>. | #Достаём из очереди множество <tex>\{1, 2\}</tex>: <tex>Q = \{\}</tex>. | ||
| Строка 53: | Строка 53: | ||
#Помечаем все терминальные вершины, в данном случае — <tex>\{1, 2\}</tex>. | #Помечаем все терминальные вершины, в данном случае — <tex>\{1, 2\}</tex>. | ||
| − | В итоге получаем ДКА, эквивалентный исходному: [[Файл:NKA_algorithm. | + | В итоге получаем ДКА, эквивалентный исходному: [[Файл:NKA_algorithm.png]]. |
[[Категория: Теория формальных языков]] | [[Категория: Теория формальных языков]] | ||
[[Категория: Автоматы и регулярные языки]] | [[Категория: Автоматы и регулярные языки]] | ||
Версия 06:01, 21 января 2012
Содержание
Построение эквивалентного ДКА по НКА
Пусть нам дан произвольный НКА: .
Построим по нему следующий ДКА: , где:
- ,
- ,
- ,
- .
Доказательство эквивалентности
| Теорема: |
Построенный ДКА эквивалентен данному НКА. |
| Доказательство: |
|
Алгоритм Томпсона
Данный алгоритм преобразовывает НКА в эквивалентный ДКА. Будем использовать вышеуказанный способ построения с одним дополнением — не будем учитывать состояния недостижимые из стартового. Поэтому в алгоритме используется обход в ширину.
Алгоритм
— очередь состояний, соответствующих множествам, состоящих из состояний НКА. — стартовое состояние НКА.
.push({}) while not isEmpty() .pop() for = for = if ( haven't been in ) .push()
Асимптотика
Так как количество подмножеств множества состояний НКА не более, чем , а каждое подмножество мы обрабатываем ровно один раз за время , получаем верхнюю оценку времени работы алгоритма — .
Пример
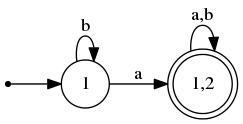
Пусть нам дан недетерменированный конечный автомат: 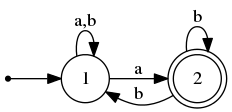
По нашему заданию эквивалентного ДКА мы получаем: 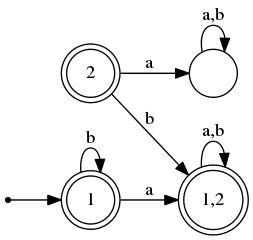
- Помещаем в очередь множество из одной стартовой вершины — : .
- Достаём из очереди множество : .
- , кладём множество в очередь: .
- , нам не надо класть множество в очередь, так как оно уже там было.
- Достаём из очереди множество : .
- , нам не надо класть множество в очередь, так как оно уже там было.
- , нам не надо класть множество в очередь, так как оно уже там было.
- Помечаем все терминальные вершины, в данном случае — .