Укладка дерева — различия между версиями
м |
|||
| Строка 5: | Строка 5: | ||
Существуют несколько способов укладки дерева на плоскости. | Существуют несколько способов укладки дерева на плоскости. | ||
=== Поуровневая укладка === | === Поуровневая укладка === | ||
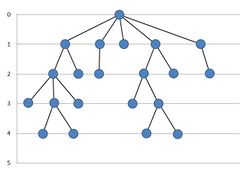
| − | Простой способ построения нисходящего плоского изображения дерева заключается в использовании его поуровневого расположения (''layered drawing''), при котором вершины глубины <tex>a</tex> имеют координату <tex>y = – a</tex>, а координаты по горизонтальной оси распределяются так, чтобы никакие левые поддеревья не пересекались с правыми (см. рисунок 1). Возможна реализация за линейное время, позволяющая получить оптимальное по ширине плоское дерево в области размера <tex>O(N^2)</tex> (где <tex>N</tex> — число вершин дерева). | + | Простой способ построения нисходящего плоского изображения дерева заключается в использовании его поуровневого расположения (''layered drawing''), при котором вершины глубины <tex>a</tex> имеют координату <tex>y = – a</tex>, а координаты по горизонтальной оси распределяются так, чтобы никакие левые поддеревья не пересекались с правыми (см. рисунок 1). Возможна реализация за линейное время, позволяющая получить оптимальное по ширине [[Укладка графа на плоскости|плоское дерево]] в области размера <tex>O(N^2)</tex> (где <tex>N</tex> — число вершин дерева). |
=== Радиальная поуровневая укладка === | === Радиальная поуровневая укладка === | ||
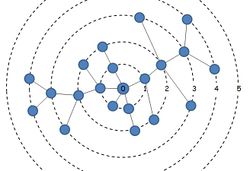
[[Файл:Circle_layered_tree.jpg|250px|right|thumb|Рисунок 2. Граф из рисунка 1, но уложенный радиально.]] | [[Файл:Circle_layered_tree.jpg|250px|right|thumb|Рисунок 2. Граф из рисунка 1, но уложенный радиально.]] | ||
| − | Радиальная поуровневая укладка(''radial drawing'') дерева отличается тем, что его уровни имеют вид концентрических окружностей | + | Радиальная поуровневая укладка(''radial drawing'') дерева отличается тем, что его уровни имеют вид концентрических окружностей (см. рисунок 2). |
| − | + | Вершины глубины <tex>a</tex> располагаются на окружностях с радиусом <tex>r = a</tex>, при этом каждое поддерево находится внутри некоторого сектора (то есть между двумя лучами исходящими из центра). | |
| + | Определим способ выбора угла этого сектора для некоторого поддерева вершины <tex>p</tex> находящейся на уровне <tex>i</tex>. Пусть угол сектора для дерева с корнем <tex>p</tex> равен <tex>\beta_p</tex>. Пусть корень поддерева(и непосредственный ребенок <tex>p</tex>) - вершина <tex>q</tex>, обозначим количество вершин в дереве с корнем <tex>q</tex> как <tex>l(q)</tex>. | ||
| + | Тогда <tex>\beta_q = \min(\frac{l(q)}{l(p)}\beta_p, \tau)</tex>, где <tex>\tau</tex> — это угол области <tex>F_p</tex>, определяемой пересечением касательной к окружности уровня <tex>i</tex> в точке <tex>p</tex> и окружностью уровня <tex>i+1</tex>. Угол <tex>\tau</tex> необходим для того, чтобы отрезок <tex>pq</tex> не пересек окружность уровня <tex>i</tex>. | ||
| − | Радиальное изображение дерева часто используют для представления свободных деревьев, причем в качестве вершины, размещаемой в центре, берется одна из его центральных вершин <ref name="Центральная вершина">Центральная вершина - эта такая вершина, для которой расстояние от которой до самой удаленной вершины - минимальное среди всех вершин графа. Формально: Пусть <tex>r(p) = \underset{u:u\in V(G)}{sup} dist(p, u)</tex>, тогда <tex>p</tex> - центральная, если <tex>r(p) = \underset{v:v\in V(G)}{inf} r(v)</tex>. Понятно, что таких вершин может быть несколько. Под расстоянием здесь подразумевается длина кратчайшего пути.</ref>. | + | Радиальное изображение дерева часто используют для представления свободных деревьев<ref name = "Свободное дерево">Под свободными деревьями(''free trees'') понимают деревья без выделенного корня. </ref>, причем в качестве вершины, размещаемой в центре, берется одна из его центральных вершин <ref name="Центральная вершина">Центральная вершина - эта такая вершина, для которой расстояние от которой до самой удаленной вершины - минимальное среди всех вершин графа. Формально: Пусть <tex>r(p) = \underset{u:u\in V(G)}{sup} dist(p, u)</tex>, тогда <tex>p</tex> - центральная, если <tex>r(p) = \underset{v:v\in V(G)}{inf} r(v)</tex>. Понятно, что таких вершин может быть несколько. Под расстоянием здесь подразумевается длина кратчайшего пути.</ref>. |
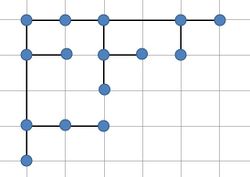
[[Файл:Hv_tree.jpg|250px|left|thumb|Рисунок 3. Пример укладки двоичного дереве в виде hv-изображения.]] | [[Файл:Hv_tree.jpg|250px|left|thumb|Рисунок 3. Пример укладки двоичного дереве в виде hv-изображения.]] | ||
=== hv-изображения === | === hv-изображения === | ||
| − | Бинарные деревья можно изобразить при помощи hv-изображений (''horizontal-vertical drawing'', см. рисунок 3). При этом для каждой вершины <tex>p</tex> выполняются следующие свойства: | + | Бинарные деревья<ref name = "Бинарное дерево">Бинарное дерево (двоичное дерево, ''binary tree''), то есть такое дерево, у каждой вершины которого не более двух поддеревьев.</ref> можно изобразить при помощи hv-изображений (''horizontal-vertical drawing'', см. рисунок 3). При этом для каждой вершины <tex>p</tex> выполняются следующие свойства: |
* сын вершины <tex>p</tex> ставится в ряд за <tex>p</tex> либо по горизонтали справа, либо по вертикали вниз | * сын вершины <tex>p</tex> ставится в ряд за <tex>p</tex> либо по горизонтали справа, либо по вертикали вниз | ||
* два прямоугольника, ограничивающие левое и правое поддерево вершины <tex>p</tex> не пересекаются | * два прямоугольника, ограничивающие левое и правое поддерево вершины <tex>p</tex> не пересекаются | ||
Версия 16:53, 7 февраля 2012
Дерево — планарный граф. Его планарность можно подтвердить, предъявив способ укладки для произвольного дерева. По формуле Эйлера: .
Содержание
Укладка дерева
Существуют несколько способов укладки дерева на плоскости.
Поуровневая укладка
Простой способ построения нисходящего плоского изображения дерева заключается в использовании его поуровневого расположения (layered drawing), при котором вершины глубины имеют координату , а координаты по горизонтальной оси распределяются так, чтобы никакие левые поддеревья не пересекались с правыми (см. рисунок 1). Возможна реализация за линейное время, позволяющая получить оптимальное по ширине плоское дерево в области размера (где — число вершин дерева).
Радиальная поуровневая укладка
Радиальная поуровневая укладка(radial drawing) дерева отличается тем, что его уровни имеют вид концентрических окружностей (см. рисунок 2).
Вершины глубины располагаются на окружностях с радиусом , при этом каждое поддерево находится внутри некоторого сектора (то есть между двумя лучами исходящими из центра). Определим способ выбора угла этого сектора для некоторого поддерева вершины находящейся на уровне . Пусть угол сектора для дерева с корнем равен . Пусть корень поддерева(и непосредственный ребенок ) - вершина , обозначим количество вершин в дереве с корнем как . Тогда , где — это угол области , определяемой пересечением касательной к окружности уровня в точке и окружностью уровня . Угол необходим для того, чтобы отрезок не пересек окружность уровня .
Радиальное изображение дерева часто используют для представления свободных деревьев[1], причем в качестве вершины, размещаемой в центре, берется одна из его центральных вершин [2].
hv-изображения
Бинарные деревья[3] можно изобразить при помощи hv-изображений (horizontal-vertical drawing, см. рисунок 3). При этом для каждой вершины выполняются следующие свойства:
- сын вершины ставится в ряд за либо по горизонтали справа, либо по вертикали вниз
- два прямоугольника, ограничивающие левое и правое поддерево вершины не пересекаются
Примечания
- ↑ Под свободными деревьями(free trees) понимают деревья без выделенного корня.
- ↑ Центральная вершина - эта такая вершина, для которой расстояние от которой до самой удаленной вершины - минимальное среди всех вершин графа. Формально: Пусть , тогда - центральная, если . Понятно, что таких вершин может быть несколько. Под расстоянием здесь подразумевается длина кратчайшего пути.
- ↑ Бинарное дерево (двоичное дерево, binary tree), то есть такое дерево, у каждой вершины которого не более двух поддеревьев.