Очередь

Определение

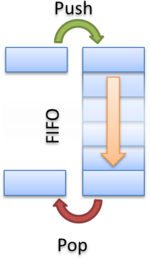
Очередь (Queue)  — это динамическое множество, добавление и удаление элементов в котором происходит путём операций Push и Pop соответственно. Притом первым из очереди удаляется элемент, который был помещен туда первым, то есть в очереди реализуется принцип «первым вошел — первым вышел» (first-in, first-out — FIFO). Очередь подобна, например, живой очередь в магазине за хлебом. У нее имеется голова (head) и хвост (tail). Когда элемент ставится в очередь, он занимает место в её хвосте, точно так же, как человек занимает очередь последним, чтобы купить хлеб. Из очереди всегда выводится элемент, который находится в её головной части аналогично тому, как человек, который ждал дольше всех, расплачивается за хлеб.

• [math]push[/math] (запись в очередь) - операция вставки нового элемента.
• [math]pop[/math] (снятие с очереди) - операция удаления нового элемента.
• [math]empty[/math] - проверка очереди на наличие в ней элементов

Реализация на массиве

Очередь, способную вместить не более [math]n[/math] элементов, можно реализовать с помощью массива [math]elements[1..n][/math]. Она будет обладать следующими полями:

[math]head[/math] (голова очереди)

[math]tail[/math] (хвост очереди)

[math]size[/math] (размер очереди)

push

push(x)
    elements[tail] = x
    tail = (tail + 1) % elements.length
    size++

pop

pop()
    if (!empty()) 
        then x = elements[head]
             head = (head + 1) % elements.length
             size--
             return x

empty

empty()
    return size == 0

Каждая операция выполняется в течение времени [math]O(1)[/math].

Плюсы:

- прост в разработке

- по сравнению с реализацией на списке, есть незначительная экономия памяти

Минусы:

- количество элементов в очереди ограничено размером массива (исправляется написанием функции расширения массива)

- при переполнении очереди требуется перевыделение памяти и копирование всех элементов в новый массив

Реализация на списке

Для данной реализации очереди необходимо создать список ([math]list[/math]) и операции работы на созданном списке.

Реализация очереди на односвязном списке:

list

• [math]x.value[/math] - поле, в котором хранится значение элемента
• [math]x.next[/math] - указатель на следующий элемент очереди

push

push(x)
    el = tail
    tail.value = x
    tail.next = null
    if (size == 0)
        then head = tail
        else el.next = tail
    size++

pop

pop()
   if (!empty()) 
       then x = head.value
            head = head.next
            size--
            return x

empty

empty()
    return size == 0

Каждая операция выполняется в течение времени [math]O(1)[/math].

Минусы:

• память фрагментируется гораздо сильнее и последовательная итерация по такой очереди может быть ощутимо медленнее, нежели итерация по очереди реализованной на массиве

Реализация на двух стеках

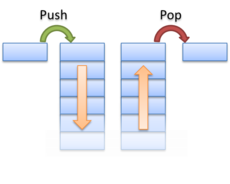
Очередь можно реализовать на двух стеках [math]leftStack[/math] и [math]rightStack[/math]. Один из стеков [math](leftStack)[/math] будем использовать для операции [math]push[/math], другой для операции [math]pop[/math].

push

push(x)
    leftStack.push(x)

pop

pop()
    if (rightStack.empty())
        then if (!leftStack.empty())
             then while (!leftStack.empty())
                      do rightStack.push(leftStack.pop)
    return rightStack.pop()

См. также

• Стек

Ссылки

• Википедия - Очередь (программирование)