СНМ(списки с весовой эвристикой)

Определение

Определение:

Весовая эвристика(weighted-union heuristic) - улучшение наивной реализации СНМ, при котором список включает поле длины списка, и добавление идет всегда меньшего списка к большему.

Проблема наивной реализации

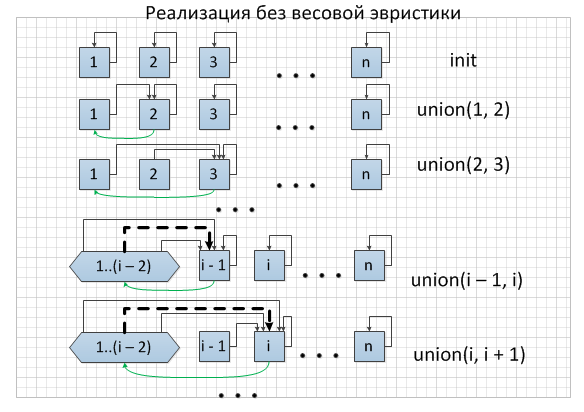
Рассмотрим модифицированную наивную реализацию системы непересекающихся множеств с помощью списка. Кроме ссылок на следующий элемент будем хранить ссылку на представителя, а для представителя ссылку на голову списка. При использовании такого представления, время работы процедур makeSet и findSet — [math]O(1)[/math]. Процедуру union(x, y) мы выполняем, добавляя список с элементом x в список содержащий элемент y. При этом мы должны обновить указатели на представителя у каждого объекта, который содержался в списке, содержащем x. Не трудно привести последовательность из m операций над n объектами, которая требует [math]O(n^2)[/math] времени. Предположим, что у нас есть объекты [math]x_1, x_2, ... x_n[/math]. Мы выполняем последовательность из n операций makeSet(или init), за которой следует последовательность из n - 1 операции union. m = n + (n - 1) = 2n - 1. На выполнение n операций makeSet мы тратим время [math]O(n)[/math]. Поскольку i-я операция union обновляет i объектов, общее количество объектов, обновленных всеми n - 1 операциями union равно [math]\sum\limits_{i=1}^{n-1} i = O(n^2)[/math]. Общее количество операций равно 2n - 1, так что каждая операция в среднем требует для выполнения [math]O(n)[/math]. Таким образом амортизированное время выполнения операции union составляет [math]O(n)[/math]. В худшем случае представленная реализация процедуры union требует в среднем [math]O(n)[/math] времени на вызов, поскольку может оказаться, что мы присоединяем длинный список к короткому и должны при этом обновить поля указателей на представителя всех членов длинного списка.

Реализация с весовой эвристикой

Предположим теперь, что каждый список включает также поле длины списка и что мы всегда добавляем меньший список к большему(при одинаковых длинах порядок добавления безразличен). При такой простейшей весовой эвристике одна операция union может потребовать [math]\Omega(n)[/math] действий, если оба множества имеют [math]\Omega(n)[/math] членов. Однако последовательность из m операций makeSet, union и findSet, n из которых составляют операции makeSet, требует для выполнения [math]O(m + n \log n)[/math] времени.

Доказательство оценки времени выполнения

Утверждение:

При использовании связанных списков для представления СНМ и применении весовой эвристики, последовательность из m операций makeSet, union, и findSet, n из которых составляют операции makeSet, требует для выполнения [math]O(m+n \log n)[/math] времени.

[math]\triangleright[/math]

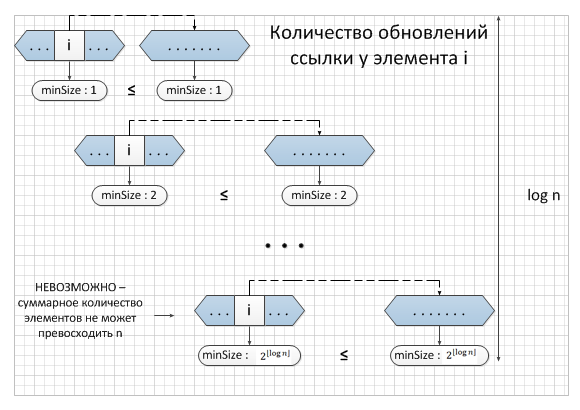
Вычислим верхнюю границу количества обновлений указателя на представителя для каждого множества из n элементов. Рассмотрим некий фиксированный объект. Когда мы обновляем указатель на представителя в объекте, он должен находиться в меньшем из множеств. Следовательно, при первом обновлении образованное множество хранит не менее 2 элементов, при втором не менее 4 элементов, и т.д. Продолжая рассуждение приходим к выводу о том, что при k [math]\leqslant\[/math] n, после того как указатель на представителя в объекте обновлен [math]\left\lceil \log k \right\rceil[/math], полученное в результате множество должно иметь не менее k элементов. Поскольку максимальное множество может иметь не более n элементов, во всех операциях union указатель на представителя у каждого объекта может быть обновлен не более [math]\left\lceil \log n \right\rceil[/math] раз. Необходимо также отметить, что обновление указателя на голову и next представителя, а также обновление длины списка при выполнении операции union требует [math]O(1)[/math] времени. Таким образом, общее время, необходимое для обновления n объектов, составляет [math]O(n \log n)[/math]. Отсюда легко понять, что время необходимое для выполнения всей последовательности из m операций составит [math]O(m + n \log n)[/math]. [math]O(m)[/math] операций makeSet и findSet, работающих за константное время и суммарное время работы операций union для каждого объекта.

[math]\triangleleft[/math]

Другие реализации

• СНМ(наивные реализации)
• СНМ(реализация с помощью леса корневых деревьев)

Источники

• Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ — 2-е изд. — М.: «Вильямс», 2007. — с. 585—588. — ISBN 5-8489-0857-4

Ссылки

• Система непересекающихся множеств и её применения