Применение метода четырёх русских в задачах ДП на примере задачи о НОП

Описание алгоритма

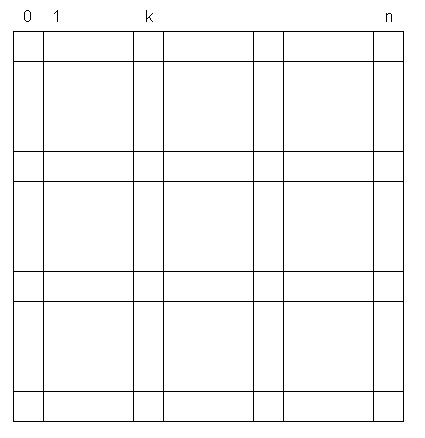
Рассмотрим задачу о наибольшей общей подпоследовательности для двух последовательностей одинаковой длины. Тогда таблица динамического программирования имеет размер [math] (n + 1) \times (n + 1) [/math]. Разобьём её на квадраты размера [math] k \times k [/math] следующим образом: выделим каждую [math] k [/math]-ую строчку, начиная с первой. Аналогично выделяем столбцы.

Требуется, чтобы [math] k [/math] делило [math] n [/math], но это не является ограничением - можно дописать в конец последовательностей символы, которые не встречались в других местах этих последовательностей (символы для каждой последовательности должны быть разными). Тогда ответ на задачу не изменится, а длину можно "довести" до делителя [math] k [/math].

Сделаем предподсчёт действия каждого возможного квадрата. Окончательный результат зависит только от значений в верхнем левом "уголке" квадрата и подстрок, для которых считается ответ — остальные значения в квадрате однозначно считаются с их помощью. Окончательным результатом будут значения в нижнем правом "уголке" квадрата.

Может показаться, что таких уголков может быть много. Но, так как соседние числа в матрице отличаются не более, чем на один, то результат зависит только от константы в верхнем левом элементе матрицы, и возрастания чисел в верхнем и левом крае квадрата. Возрастание чисел будем хранить с помощью битовых масок: сначала [math] k - 1 [/math] бит кодирует возрастание чисел в верхнем крае квадрата (0 - элемент равен предыдущему, 1 - больше предыдущего на один), потом [math] k - 1 [/math] бит кодируют возрастание чисел в квадрате по левому краю аналогичным образом.

Более того, константу в верхнем левом элементе квадрата можно вообще не хранить - её можно прибавить при необходимости к каждому элементу результата.

После этого ответ для самой задачи НОП считается аналогично обычному алгоритму, только на этот раз пересчитывается не каждый элемент матрицы, а только уголки.

Время работы

При предподсчёте перебирается [math] | \Sigma | ^k [/math] (где [math] | \Sigma | [/math] — мощность алфавита) возможных подстрок первой строки и столько же — второй строки. Для каждой возможной подстроки обеих строк перебирается по [math] 2^{k - 1} [/math] битовых масок. Для самого предподсчёта требуется время [math] O(k^2) [/math]. Дальнейший алгоритм поиска НОП требует [math] O \left ( \frac{n^2}{k^2} \right ) [/math]. Тогда суммарное время работы алгоритма составляет [math] O \left ( |\Sigma| ^{2k} \cdot 2^{2k - 2} \cdot k^2 + \frac{n^2}{k^2} \right ) [/math]. Понятно, что для получения выигрыша в производительности по сравнению с обычным алгоритмом необходимо, чтобы первое слагаемое не превышало второе. Найдём [math] k [/math], решив неравенство [math] |\Sigma| ^{2k} \cdot 2^{2k - 2} \cdot k^2 \leqslant \frac{n^2}{k^2} [/math]. Оно преобразуется к виду [math] \left ( 2 | \Sigma | \right ) ^{2k} \cdot \frac{1}{4} \cdot k^4 \leqslant n^2 [/math]. Далее извлекаем корень: [math] \left ( 2 | \Sigma | \right ) ^k \cdot k^2 \leqslant 2n [/math]. Прологарифмируем: [math] k \log {2 | \Sigma |} + 2 \log k \leqslant \log 2 + \log n [/math]. Отсюда [math] k \lt \frac{\log n}{\log {1 + | \Sigma |}}[/math]

Источники

• http://pages.cpsc.ucalgary.ca/~pmohasse/private-lcs.pdf