АВЛ-дерево — различия между версиями
(→Высота дерева) |
(→Слияние двух AVL-деревьев) |
||
| Строка 151: | Строка 151: | ||
| − | [[Файл: | + | [[Файл: Navltree1.jpg]] |
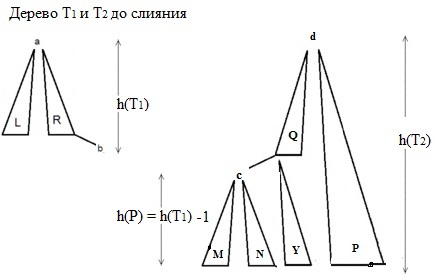
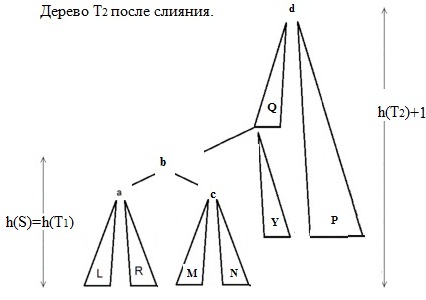
В дереве <tex>T_1</tex> удаляем самую правую вершину, назовём её <tex>b</tex>. Высота дерева <tex>T_1</tex> может уменьшиться на единицу. В дереве <tex>T_2</tex> идём от корня всегда в левое поддерево и, когда высота этого поддерева <tex>P</tex> будет равна высоте дерева <tex>T_1</tex>, делаем новое дерево <tex>S</tex>, корнем <tex>S</tex> будет вершина <tex>b</tex>, левым поддеревом будет дерево <tex>T_1</tex>, а правым дерево <tex>P</tex>. Теперь в дереве <tex>T_2</tex> у вершины, в которой мы остановились при спуске, левым поддеревом делаем дерево <tex>S</tex> и запускаем балансировку. Таким образом, дерево <tex>T_2</tex> будет результатом слияния двух АВЛ-деревьев. | В дереве <tex>T_1</tex> удаляем самую правую вершину, назовём её <tex>b</tex>. Высота дерева <tex>T_1</tex> может уменьшиться на единицу. В дереве <tex>T_2</tex> идём от корня всегда в левое поддерево и, когда высота этого поддерева <tex>P</tex> будет равна высоте дерева <tex>T_1</tex>, делаем новое дерево <tex>S</tex>, корнем <tex>S</tex> будет вершина <tex>b</tex>, левым поддеревом будет дерево <tex>T_1</tex>, а правым дерево <tex>P</tex>. Теперь в дереве <tex>T_2</tex> у вершины, в которой мы остановились при спуске, левым поддеревом делаем дерево <tex>S</tex> и запускаем балансировку. Таким образом, дерево <tex>T_2</tex> будет результатом слияния двух АВЛ-деревьев. | ||
| − | [[Файл: | + | [[Файл: Navltree2.jpg]] |
== Литература == | == Литература == | ||
Версия 19:32, 1 апреля 2012
АВЛ-дерево — сбалансированное двоичное дерево поиска, в котором поддерживается следующее свойство: для каждой его вершины высота её двух поддеревьев различается не более чем на 1.
АВЛ-деревья названы по первым буквам фамилий их изобретателей, Г. М. Адельсона-Вельского и Е. М. Ландиса, которые впервые предложили использовать АВЛ-деревья в 1962 году.
Содержание
Высота дерева
| Теорема: | ||||||
АВЛ-дерево с ключами имеет высоту . | ||||||
| Доказательство: | ||||||
|
Высоту поддерева с корнем будем обозначать как , высоту поддерева — как .
Логарифмируя по основанию , получаем Таким образом, получаем, что высота AVL-дерева из n вершин — . | ||||||
Балансировка
Балансировкой вершины называется операция, которая в случае разницы высот левого и правого поддеревьев , изменяет связи предок-потомок в поддереве данной вершины так, чтобы восстановилось свойство дерева , иначе ничего не меняет. Для балансировки будем хранить для каждой вершины разницу между высотой её левого и правого поддерева
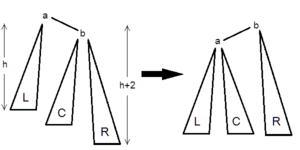
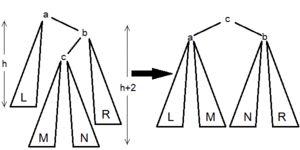
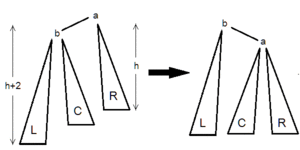
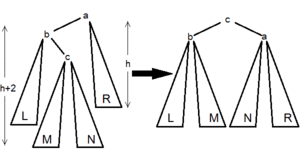
Для балансировки вершины используются один из 4 типов вращений:
В каждом случае операция приводит к нужному результату, а полная высота уменьшается не более чем на 1 и не может увеличиться.
Все операции вращения, очевидно, требуют операций.
Операции
Добавление вершины
Пусть нам надо добавить ключ . Будем спускаться по дереву, как при поиске ключа . Если мы стоим в вершине и нам надо идти в поддерево, которого нет, то делаем ключ листом, а вершину его корнем. Дальше поднимаемся вверх по пути поиска и пересчитываем баланс у вершин. Если мы поднялись в вершину из левого поддерева, то увеличивается на единицу, если из правого, то уменьшается на единицу. Если пришли в вершину и её баланс стал равным нулю, то это значит высота поддерева не изменилась и подъём останавливается. Если пришли в вершину и её баланс стал равным 1 или -1, то это значит высота поддерева изменилась и подъём продолжается. Если пришли в вершину и её баланс стал равным 2 или -2, то делаем одно из четырёх вращений и, если после вращения баланс стал равным нулю, то останавливаемся, иначе продолжаем подъём.
Так как в процессе добавления вершины мы рассматриваем не более, чем вершин дерева, и для каждой запускаем балансировку не более одного раза, то суммарное количество операций при включении новой вершины в дерево составляет операций.
Удаление вершины
Для простоты опишем рекурсивный алгоритм удаления. Если вершина - лист, то удалим её, иначе найдём самую близкую по значению вершину , переместим её на место удаляемой вершины и удалим вершину . От удалённой вершины будем подниматься вверх к корню и пересчитывать баланс у вершин. Если мы поднялись в вершину из левого поддерева, то уменьшается на единицу, если из правого, то увеличивается на единицу. Если пришли в вершину и её баланс стал равным 1 или -1, то это значит, что высота этого поддерева не изменилась и подъём можно остановить. Если баланс вершины стал равным нулю, то высота поддерева уменьшилась и подъём нужно продолжить. Если баланс стал равным 2 или -2, следует выполнить одно из четырёх вращений и, если после вращений баланс вершины стал равным нулю, то подъём продолжается, иначе останавливается.
В результате указанных действий на удаление вершины и балансировку суммарно тратится, как и ранее, операций. Таким образом, требуемое количество действий — .
Поиск вершины, минимум/максимум в дереве, etc.
Остальные операции не меняют структуры дерева, поэтому выполняются так же, как и в наивной реализации дерева поиска.
Слияние двух AVL-деревьев
Дано два дерева и , все ключи в меньше ключей в , .
В дереве удаляем самую правую вершину, назовём её . Высота дерева может уменьшиться на единицу. В дереве идём от корня всегда в левое поддерево и, когда высота этого поддерева будет равна высоте дерева , делаем новое дерево , корнем будет вершина , левым поддеревом будет дерево , а правым дерево . Теперь в дереве у вершины, в которой мы остановились при спуске, левым поддеревом делаем дерево и запускаем балансировку. Таким образом, дерево будет результатом слияния двух АВЛ-деревьев.