Турниры — различия между версиями
м |
м |
||
| Строка 6: | Строка 6: | ||
{| class="wikitable" style="border-spacing: 10px;" | {| class="wikitable" style="border-spacing: 10px;" | ||
| − | |<center>[[Файл:Tournament_1_2.png| | + | |<center>[[Файл:Tournament_1_2.png|135px]]</center> || <center>[[Файл:Tournament_1_3.png|410px]]</center> |
|- | |- | ||
| − | |colspan="2" |[[Файл:Tournament_1_4.png| | + | |colspan="2" |[[Файл:Tournament_1_4.png|690px]] |
|- | |- | ||
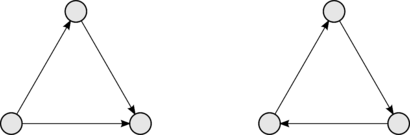
!colspan="2" |<center>Турниры из 2, 3 и 4 вершин</center> | !colspan="2" |<center>Турниры из 2, 3 и 4 вершин</center> | ||
| Строка 24: | Строка 24: | ||
{| class="wikitable" style="float:right; border-spacing: 10px;" | {| class="wikitable" style="float:right; border-spacing: 10px;" | ||
| − | |<center>[[Файл:Tournament_2.png| | + | |<center>[[Файл:Tournament_2.png|380px]]</center> |
|- | |- | ||
!|<center>Негамильтонов турнир</center> | !|<center>Негамильтонов турнир</center> | ||
Версия 20:10, 23 апреля 2012
| Определение: |
| Турнир — ориентированный граф, между любой парой различных вершин которого есть ровно одно ориентированное ребро. |
Название этого класса графов связано с тем, что их удобно использовать для описания результатов командных соревнований в некоторых видах спорта.
 | |

| |
Сильно связные турниры
| Определение: |
| Турнир называется сильно связным, если из любой вершины существуют пути до всех других. |
| Определение: |
| Турнир называется гамильтоновым, если он содержит гамильтонов цикл. |
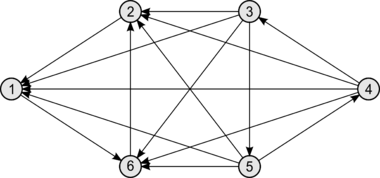 |
Не все турниры гамильтоновы. Определение не исключает существование вершины с полустепенью исхода или захода равной нулю — в первую нельзя войти, а из второй — выйти. Однако отсутствие таких вершин не означает, что турнир гамильтонов (пример — на рисунке справа).
Теорема Редеи-Камиона устанавливает 2 следующих факта:
- Все турниры полугамильтоновы.
- Турнир гамильтонов тогда и только тогда, когда он сильно связен.
См. также
Литература
- Асанов М. О., Баранский В. А., Расин В. В. Дискретная математика: графы, матроиды, алгоритмы — НИЦ РХД, 2001. — ISBN 5-93972-076-5