Участник:Muravyov

Триангуляция полигона — декомпозиция многоугольника [math]P[/math] на множество треугольников, внутренние области которых попарно не пересекаются и объединение которых в совокупности составляет [math]P[/math]. В строгом смысле слова, вершины этих треугольников должны совпадать с вершинами исходного многоугольника. Триангуляция любого многоугольника не единственна. В этом можно убедиться из примера на рисунке.

Постановка задачи

На плоскости задан произвольный многоугольник. Стороны многоугольника не пересекаются. Требуется найти его триангуляцию.

Теорема о существовании трингуляции

Простым многоугольником является фигура, ограниченная одной замкнутой ломаной, стороны которой не пересекаются. Таким образом, случаи многоугольников с дырками в теореме исключаются.

Теорема (О существовании триангуляции многоугольника):

У любого простого [math]n[/math]-вершинного многоугольника [math]P[/math] всегда существует триангуляция, причём количество треугольников в ней [math]n - 2[/math] независимо от самой триангуляции.

Доказательство:

[math]\triangleright[/math]

Доказательство ведётся индуктивно по [math]n[/math]. При [math]n = 3[/math] теорема тривиальна. Рассмотрим случай при [math]n \gt 3[/math] и предположим, что теорема выполняется при всех [math]m \lt n[/math]. Докажем существование диагонали в многоугольнике [math]P[/math]. Возьмём самую левую по оси [math]x[/math] вершину [math]v[/math] многоугольника [math]P[/math] и две смежных с ней вершины [math]u[/math] и [math]w[/math]. Если отрезок [math]uw[/math] принадлежит внутренней области [math]P[/math] — мы нашли диагональ. В противном случае, во внутренней области треугольника [math]\Delta uwv[/math] или на самом отрезке [math]uw[/math] содержится одна или несколько вершин [math]P[/math]. Выберем самую наиболее далеко отстоящую от [math]uw[/math] вершину [math]v'[/math]. Отрезок, соединяющий [math]v[/math] и [math]v'[/math] не может пересекать сторон [math]P[/math], поскольку в противном случае одна из вершин это отрезка будет располагаться дальше от [math]uw[/math], чем [math]v'[/math]. Это противоречит условию выбора [math]v'[/math]. В итоге получаем, что [math]v'v[/math] — диагональ. Любая диагональ делит [math]P[/math] на два многоугольника [math]P_1[/math] и [math]P_2[/math]. За [math]m_1[/math] и [math]m_2[/math] обозначим количество вершин в [math]P_1[/math] и [math]P_2[/math] соответственно. [math]m_1 \lt n[/math] и [math]m_2 \lt n[/math], поэтому по предположению индукции у [math]P_1[/math] и [math]P_2[/math] существует триангуляция, следовательно и у [math]P[/math] она существует. Докажем, что триангуляция [math]P[/math] состоит из [math]n - 2[/math] треугольников. Рассмотрим произвольную диагональ [math]d[/math] в триангуляции [math]T_P[/math]. [math]d[/math] делит [math]P[/math] на два многоугольника [math]P_1[/math] и [math]P_2[/math], количество вершин в которых [math]m_1[/math] и [math]m_2[/math] соответственно. Каждая вершина [math]P[/math] встречается только в одном из двух многоугольников [math]P_1[/math] и [math]P_2[/math], за исключением тех, которые являются концами [math]d[/math], поэтому справедливо следующее: [math]m_1 + m_2 = n + 2[/math]. По индукции, любая триангуляция [math]P_i[/math] состоит из [math]m_i - 2[/math] треугольников, откуда следует, что [math]T_P[/math]. состоит из [math](m_1 - 2) + (m_2 - 2) = n - 2[/math] треугольников.

[math]\triangleleft[/math]

Способы нахождения триангуляции

Примитивный алгоритм

В общем случае в произвольном [math]n[/math]-угольнике всего [math]n^2[/math] возможных вариантов построения диагоналей. За [math]\mathcal{O}(n)[/math] проверим каждый из них. Для этого выясним:

• пересекает ли данная диагональ многоугольник — находится за линейное время проверкой по всем рёбрам
• принадлежит ли диагональ внутренней область многоугольника.

Чтобы построить триангуляцию нужно найти [math]n - 3[/math] диагоналей. В результате получается оценка [math]\mathcal{O}(n^4)[/math].

Для некоторых классов многоугольников предыдущую оценку можно улучшить. Например, если многоугольник выпуклый, то достаточно лишь выбирать одну его вершину и соединять со всеми остальными, кроме его соседей. В итоге оценка [math]\mathcal{O}(n)[/math].

Монотонный метод

Определение:

Простой многоугольник [math]P[/math] называется монотонным относительно прямой [math]l[/math], если любая [math]l'[/math], такая что [math]l' \perp l[/math], пересекает стороны [math]P[/math] не более двух раз.

Определение:

Многоугольник, монотонный относительно [math]y[/math]-оси называется [math]y[/math]-монотонным.

Идея данного метода заключается в том, чтобы разбить многоугольник на монотонные части, а затем триангулировать каждую из них.

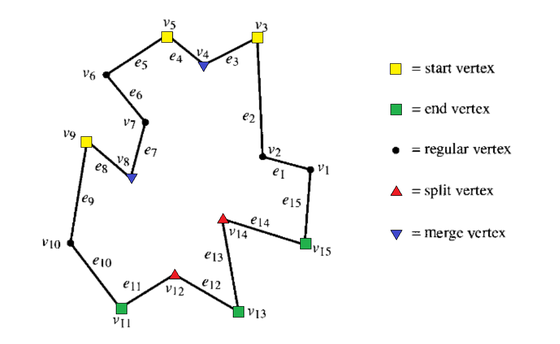
Рассмотрим самую верхнюю — максимальную по оси [math]y[/math] вершину. Будем идти вниз по рёбрам до самой нижней — соотвественно минимальной по [math]y[/math] вершине, то есть таким образом, что для некоторой вершины [math]j[/math]: [math]y_j \gt y_{j+1}[/math]. Поворотной назовём вершину [math]i[/math], на которой направление обхода будет меняется: [math]y_{i-1} \gt y_i[/math] и [math]y_i \lt y_{i+1}[/math]. Опишем более подробно этот тип вершин. Уточним понятния выше и ниже: точка [math]p[/math] лежит ниже точки [math]q[/math], если [math]p_y \lt q_y[/math] или если [math]p_y \lt q_y[/math] и [math]p_x \gt q_x[/math], соответственно точка [math]p[/math] лежит выше точки [math]q[/math], если [math]p_y \gt q_y[/math] или если [math]p_y = q_y[/math] и [math]p_x \lt q_x[/math]. Это было сделано для того, чтобы избежать неопределённых ситуаций с вершинами, у которых [math]y[/math]-координаты равны.

Пять типов вершин

Обозначим за [math]\phi[/math] внутренний при некоторой вершине вершине и определим далее пять типов вершин, четыре из которых являются поворотными:

• start-вершина — два её соседа лежат ниже её самой и [math] \phi \lt \pi [/math]
• split-вершина — два её соседа лежат ниже её самой и [math] \phi \gt \pi [/math]
• end-вершина — два её соседа лежат выше её самой и [math] \phi \lt \pi [/math]
• merge-вершина — два её соседа лежат выше её самой и [math] \phi \gt \pi [/math]
• regular-вершина — не является поворотной, в отличие от остальных, другими словами один её сосед находится выше, а другой ниже её самой.

Ушной метод

Более эффективным я