Классы NC и AC — различия между версиями
(→Определения) |
(→Определения) |
||
| Строка 2: | Строка 2: | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
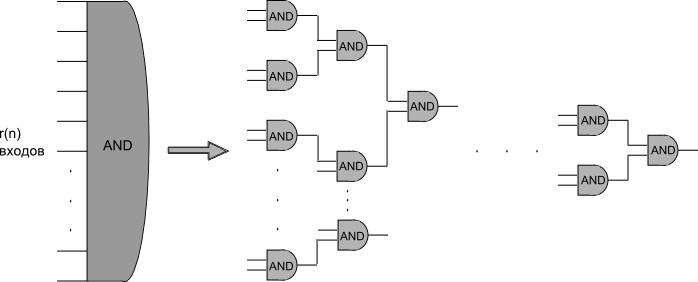
| − | <tex>NC^i = \mathcal{f} L \mid L — </tex> распознается семейством схем размера полином от <tex>n</tex> и глубины <tex>O(log^i (n))</tex>, где <tex>n</tex> — длина входа; степень входа элемента не больше двух. Причем такую схему можно построить по <tex>1^n</tex> на <tex>O(log(n))</tex> памяти. | + | <tex>NC^i = \mathcal{f} L \mid L — </tex> распознается семейством логических схем размера полином от <tex>n</tex> и глубины <tex>O(log^i (n))</tex>, где <tex>n</tex> — длина входа; степень входа элемента не больше двух. Причем такую схему можно построить по <tex>1^n</tex> на <tex>O(log(n))</tex> памяти. |
}} | }} | ||
Версия 12:47, 30 апреля 2012
Определения
| Определение: |
| распознается семейством логических схем размера полином от и глубины , где — длина входа; степень входа элемента не больше двух. Причем такую схему можно построить по на памяти. |
| Определение: |
| определяется аналогично , только степень входа элемента неограничена. |
| Определение: |
Теоремы
Следствие:
Тезис
распознается параллельным компьютером с процессоров за время .
| Теорема: |
| Доказательство: |
| Пусть . Тогда распознается некоторым семейством схем которые по можно построить на памяти и, следовательно, за полиномиальное от время. Построим для данного входа схему и вычислим ее. |