Классы NC и AC

Определения

Определение:

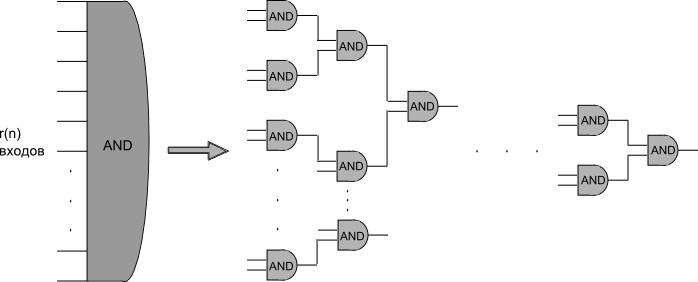
[math]NC^i = \mathcal{f} L \mid L — [/math] распознается семейством логических схем размера полином от [math]n[/math] и глубины [math]O(log^i (n))[/math], где [math]n[/math] — длина входа; степень входа элемента не больше двух. Причем такую схему можно построить по [math]1^n[/math] на [math]O(log(n))[/math] памяти.

Определение:

[math]AC^i[/math] определяется аналогично [math]NC^i[/math], только степень входа элемента неограничена.

Определение:

[math]NC = \cup^{\infty}_{i = 0} NC^i[/math] [math]AC = \cup^{\infty}_{i = 0} AC^i[/math]

Теоремы

Теорема:

[math]NC^i \subset AC^i \subset NC^{i+1}[/math]

Доказательство:

[math]\triangleright[/math]

[math]NC^i \subset AC^i[/math] Это очевидно из определения [math]NC^i[/math] и [math]AC^i[/math]. [math]AC^i \subset NC^{i+1}[/math] Пусть [math]L \in AC^i[/math]. [math]L[/math] распознается семейством схем [math]C_n[/math] полиномиального размера. Значит степень входа у элементов схемы [math]C_n[/math] это полином [math]r(n)[/math]. Заменим элементы схемы [math]C_n[/math] элементами со степенью входа не более двух следующим образом: При замене каждого такого элемента глубина будет увеличиваться на [math]log_2 r(n) = O(log(n))[/math] и размер схемы останется полиномиальным.

[math]\triangleleft[/math]

Следствие: [math]NC = AC[/math]

Теорема:

[math]NC \subseteq P[/math]

Доказательство:

[math]\triangleright[/math]

Пусть [math]L \in NC[/math]. Тогда [math]L[/math] распознается некоторым семейством схем [math]C_n[/math] которые по [math]1^n[/math] можно построить на [math]O(log(n))[/math] памяти и, следовательно, за полиномиальное от [math]n[/math] время. Построим для данного входа схему и вычислим ее.

[math]\triangleleft[/math]

Равенство [math]NC[/math] и [math]P[/math] — неразрешенная на данный момент задача.

Теорема:

[math]L[/math] распознается параллельным компьютером с [math]O(poly(n))[/math] процессоров за время [math]O(poly(log(n)) \Leftrightarrow L \in NC[/math].

Доказательство:

[math]\triangleright[/math]

Пусть [math]L \in NC[/math]. [math]L[/math] распознается семейством схем [math]C_n[/math], где [math]C_n[/math] размера [math]N=O(poly(n))[/math] и имеет глубину [math]O(log^d n)[/math]. Тогда возьмем параллельный компьютер с [math]N[/math] процессорами, где каждый из них будет играть роль одного элемента схемы. Так как компьютер параллельный, то вычисления на каждом уровне схемы будут выполнятся параллельно. Тогда получаем что всего потребуется [math]O(log^d(n))[/math] времени. Пусть [math]L[/math] распознается параллельным компьютером с [math]N=O(poly(n))[/math] процессоров за время [math]D=O(log^d n)[/math]. Тогда построим схему глубины [math]D[/math] на каждом уровне которой будет по [math]N[/math] элементов, таких, что [math]i[/math]-й элемент на уровне [math]t[/math] выполняет вычисления, производимые [math]i[/math]-го процессора в момент времени [math]t[/math].

[math]\triangleleft[/math]