Статистики на отрезках. Корневая эвристика — различия между версиями
Whiplash (обсуждение | вклад) (→Обработка запроса) |
Whiplash (обсуждение | вклад) м (→Предпосчет) |
||
| Строка 18: | Строка 18: | ||
</pre> | </pre> | ||
| − | |||
=== Обработка запроса === | === Обработка запроса === | ||
Пусть мы получили запрос на нахождение суммы (минимума/максимума и т.д) на отрезке <tex>[l, r]</tex>. Отрезок может охватить некоторые блоки массива <tex>B</tex> полностью, а так же не более двух блоков (начальный и конечный) - не полностью. | Пусть мы получили запрос на нахождение суммы (минимума/максимума и т.д) на отрезке <tex>[l, r]</tex>. Отрезок может охватить некоторые блоки массива <tex>B</tex> полностью, а так же не более двух блоков (начальный и конечный) - не полностью. | ||
Версия 23:50, 7 мая 2012
| Определение: |
| Корневая эвристика (Sqrt-декомпозиция) — это метод, или структура данных, которая позволяет выполнять некоторые ассоциативные операции над отрезками (суммирование элементов подмассива, нахождение минимума/максимума и т.д.) за . |
Содержание
Описание
Предпосчет
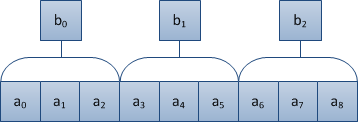
Пусть нам дан массив размерности . Cделаем следующий предпосчет:
- разделим массив на блоки длины ;
- в каждом блоке заранее предпосчитаем необходимую нам операцию (сумму элементов, минимум/максимум и т.д.);
- результаты предпосчёта запишем в массив размерности , где — количество блоков.
Пример реализации предпосчета для запроса "подсчет суммы":
for i = 0 to n
B[i / len] += A[i]
Обработка запроса
Пусть мы получили запрос на нахождение суммы (минимума/максимума и т.д) на отрезке . Отрезок может охватить некоторые блоки массива полностью, а так же не более двух блоков (начальный и конечный) - не полностью.
Таким образом, для того чтобы найти, например, сумму на отрезке нам необходимо вручную посчитать сумму на "хвостиках" и сложить с суммой полных блоков, предпосчет которых мы сделали заранее.
Пример реализации обработки запроса "подсчет суммы на отрезке " :
left = l / len
right = r / len
end = (left + 1) * len - 1
sum = 0
if left == right
for i = l to r
sum += A[i]
else
for i = l to end
sum += A[i]
for i = left + 1 to right - 1
sum += B[i]
for i = right * len to r
sum += A[i]
Запрос на изменение элемента
Для реализации данного запроса нам необходимо поменять всего два элемента, т.к. каждый элемент входит в ровно один блок массива .
Пример реализации:
- номер элемента из массива , который необходимо заменить; - на сколько нужно изменить данный элемент.
A[p] += delta B[p / len] += delta
Оценка сложности
Размер каждого из "хвостов", очевидно, не превосходит длины блока , а количество блоков не превосходит . Поскольку и , и мы выбирали , то всего для вычисления минимума и пересчитывания на отрезке нам понадобится операций.