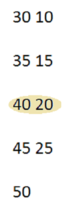Поиск k-ой порядковой статистики за линейное время — различия между версиями
| Строка 15: | Строка 15: | ||
===Особенность алгоритма=== | ===Особенность алгоритма=== | ||
Как будет доказано ниже, время работы алгоритма в наихудшем случае равно <tex>O(n)</tex>. Главная идея алгоритма заключается в том, чтобы ''гарантировать'' хорошее разбиение массива, так как чисел, которые меньше рассекающего элемента не менее <tex>\frac{3n}{10}</tex>, где <tex>n</tex> количество элементов в массиве. | Как будет доказано ниже, время работы алгоритма в наихудшем случае равно <tex>O(n)</tex>. Главная идея алгоритма заключается в том, чтобы ''гарантировать'' хорошее разбиение массива, так как чисел, которые меньше рассекающего элемента не менее <tex>\frac{3n}{10}</tex>, где <tex>n</tex> количество элементов в массиве. | ||
| + | ===Псевдокод=== | ||
| + | select(L,k) | ||
| + | { | ||
| + | if (length(L) <= 10) | ||
| + | { | ||
| + | sort L | ||
| + | return the element in the kth position //вернем элемент, находящийся на k-ой позиции; | ||
| + | } | ||
| + | partition L into subsets S[i] of five elements each //разобьем L на подмножества S[i] размером 5 по 5 элементов; | ||
| + | (there will be n/5 subsets total). | ||
| + | for (i = 1 to n/5) do | ||
| + | x[i] = select(S[i],3) //найдем медианы S[i]; | ||
| + | M = select({x[i]}, n/10) // M - рассекающий элемент; | ||
| + | partition L into L1<M, L2=M, L3>M | ||
| + | // разобьем L на подмножества L1, где все элементы меньше M, L3, где все элементы больше M и L2 равное M; | ||
| + | if (k <= length(L1)) | ||
| + | return select(L1,k) | ||
| + | else if (k > length(L1)+length(L2)) | ||
| + | return select(L3,k-length(L1)-length(L2)) | ||
| + | else return M // элемент на k-ой позиции в исходном массиве; | ||
| + | } | ||
===Пример=== | ===Пример=== | ||
На вход подается массив, разобьем элементы на группы по 5 элементов. | На вход подается массив, разобьем элементы на группы по 5 элементов. | ||
Версия 13:10, 17 мая 2012
| Определение: |
| -ой порядковой статистикой набора элементов линейно упорядоченного множества называется такой его элемент, который является -ым элементом набора в порядке сортировки |
Содержание
Историческая справка
Алгоритм Блюма-Флойда-Пратта-Ривеста-Тарьяна (BFPRT-алгоритм) создан Мануэлем Блюмом (Manuel Blum), Робертом Флойдом (Robert Floyd), Воганом Рональдом Праттом (Vaughan Ronald Pratt), Роном Ривестом (Ron Rivest) и Робертом Тарьяном (Robert Tarjan) в 1973 году.
Описание алгоритма
- Все элементов входного массива разбиваются на группы по пять элементов, в последней группе будет элементов.
- Сначала сортируется каждая группа, затем выбираем медиану в каждой из этих групп.
- Путем рекурсивного вызова шага 1 определяется медиана из множества медиан, найденных на втором шаге. - рассекающий элемент, - индекс рассекающего элемента.(Если медиан окажется четное количество, то переменной будет присвоено значение верхней медианы.)
- Делим массив относительно рассекающего элемента . Все элементы меньшие будут находиться левее в массиве и будут иметь меньший индекс и наоборот,если элементы больше .
- Если , то возвращается значение . Иначе вызывается рекурсивно шаг 1, и выполняется поиск -го в порядке возрастания элемента в левой части массива,если , или в правой части, если .
Особенность алгоритма
Как будет доказано ниже, время работы алгоритма в наихудшем случае равно . Главная идея алгоритма заключается в том, чтобы гарантировать хорошее разбиение массива, так как чисел, которые меньше рассекающего элемента не менее , где количество элементов в массиве.
Псевдокод
select(L,k)
{
if (length(L) <= 10)
{
sort L
return the element in the kth position //вернем элемент, находящийся на k-ой позиции;
}
partition L into subsets S[i] of five elements each //разобьем L на подмножества S[i] размером 5 по 5 элементов;
(there will be n/5 subsets total).
for (i = 1 to n/5) do
x[i] = select(S[i],3) //найдем медианы S[i];
M = select({x[i]}, n/10) // M - рассекающий элемент;
partition L into L1<M, L2=M, L3>M
// разобьем L на подмножества L1, где все элементы меньше M, L3, где все элементы больше M и L2 равное M;
if (k <= length(L1))
return select(L1,k)
else if (k > length(L1)+length(L2))
return select(L3,k-length(L1)-length(L2))
else return M // элемент на k-ой позиции в исходном массиве;
}
Пример
На вход подается массив, разобьем элементы на группы по 5 элементов. Отсортируем элементы каждой группы и выберем медианы. Вызовемся рекурсивно от медиан.
Разобьем на группы по 5 медианы. Отсортируем элементы каждой группы и выберем медианы
Выберем медианы медиан. В итоге мы получили один элемент равный . Это и есть рассекающий элемент.
Анализ времени работы алгоритма
Пусть - время работы алгоритма для элементов, тогда оно не больше, чем сумма:
- времени работы на сортировку групп и разбиение по рассекающему элементу, то есть ;
- времени работы для поиска медианы медиан, то есть ;
- времени работы для поиска -го элемента в одной из двух частей массива, то есть , где - количество элементов в этой части. Но не превосходит , так как чисел, меньших рассекающего элемента, не менее - это медиан, меньших медианы медиан, плюс не менее элементов, меньших этих медиан. С другой стороны, чисел, больших рассекающего элемента, так же не менее , следовательно , то есть в худшем случае .
Тогда получаем, что
Покажем, что для всех выполняется неравенство .
Докажем по индукции:
- Очевидно, что для малых выполняется неравенство
- Тогда, по предположению индукции, и , тогда
Так как , то время работы алгоритма