Цифровая сортировка

Цифровая сортировка — один из алгоритмов сортировки, использующих внутреннюю структуру сортируемых объектов.

Алгоритм

Пример цифровой сортировки трехзначных чисел

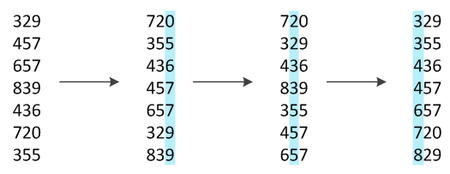
При цифровой сортировке данные разбиваются на "разряды", после чего они сортируются какой-либо устойчивой сортировкой по каждому разряду, в порядке от младшего разряда к старшему. Для чисел наиболее часто в качестве устойчивой сортировки применяют сортировку подсчетом.

Корректность алгоритма

Докажем, что данный алгоритм работает верно, используя метод математической индукции по номеру разряда. Пусть [math] n [/math] — количество разрядов в сортируемых объектах.

База: [math] n = 1 [/math]. Очевидно, что алгоритм работает верно, потому что в таком случае мы просто сортируем младшие разряды какой-то заранее выбранной стабильной сортировкой.

Переход: Пусть для [math] n = k [/math] алгоритм правильно отсортировал элементы по [math] k [/math] младшим разрядам. Покажем, что в таком случае, при сортировке по [math] (k + 1) [/math]-ому разряду, объекты также будут отсортированы в правильном порядке.

Вспомогательная сортировка разобьет все объекты на группы, в которых [math] (k + 1) [/math]-ый разряд объектов одинаковый. Рассмотрим такие группы. Для сортировки по отдельным разрядам мы используем стабильную сортировку, следовательно порядок объектов с одинаковым [math] (k + 1) [/math]-ым разрядом не изменился. Но по предположению индукции по предыдущим [math] k [/math] разрядам объекты были отсортированы правильно, и поэтому в каждой такой группе объекты будут отсортированы верно. Также верно, что сами группы находятся в правильном относительно друг друга порядке, а, следовательно, и все элементы отсортированы правильно по [math] (k + 1) [/math]-ым младшим разрядам.

Псевдокод

В качестве примера рассмотрим сортировку чисел. Как говорилось выше, в такой ситуации в качестве стабильной сортировки применяют сортировку подсчетом, так как обычно количество различных значений разрядов не превосходит количества сортируемых элементов. Ниже приведен псевдокод цифровой сортировки, которой подается массив [math] A [/math] [math] m [/math]-разрядных чисел размера [math] n [/math]. Функция [math] digit(x, i) [/math] возвращает [math] i [/math]-ый разряд числа [math] x [/math]. Так же считаем, что значения разрядов меньше [math] k [/math].

 radixSort(A)
     for i = 1 to m                                  
         for j = 0 to k - 1                             // обнуление вспомогательного массива С, 
             C[j] = 0;                                  // использующегося в качестве счетчика
         for j = 0 to n - 1
             C[digit(A[j], i)] = C[digit(A[j], i)] + 1; 
         for j = 1 to k - 1
             C[j] = C[j] + C[j - 1];
         for j = n - 1 to 0                             // заполняем вспомогательный массив B, в котором после каждой итерации
             B[C[digit(A[j], i)]] = A[j];               // внешнего цикла числа отсортированы по младшим i битам
             C[digit(A[j], i)] = C[digit(A[j], i)] - 1;
         A = B;

Сложность

Пусть [math] m [/math] — количество разрядов, [math] n [/math] — количество объектов, которые нужно отсортировать, [math] T(n) [/math] — время работы устойчивой сортировки. Цифровая сортировка выполняет [math] k [/math] итераций, на каждой из которой выполняется устойчивая сортировка и не более [math] O(1) [/math] других операций. Следовательно время работы цифровой сортировки — [math] O(k \cdot T(n)) [/math].

Рассмотрим отдельно случай сортировки чисел. Пусть в качестве аргумента сортировке передается массив, в котором содержатся [math] n [/math] [math] m [/math]-значных чисел, и каждая цифра может принимать значения от [math] 0 [/math] до [math] k - 1 [/math]. Тогда цифровая сортировка позволяет отсортировать данный массив за время [math] O(m \cdot (n + k)) [/math], если устойчивая сортировка имеет время работы [math] O(n + k) [/math]. Если [math] k [/math] небольшое, то оптимально выбирать в качестве устойчивой сортировки сортировку подсчетом.

Если количество разрядов — константа, а [math] k = O(n) [/math], то сложность цифровой сортировки составляет [math] O(n) [/math], то есть она линейно зависит от количества сортируемых чисел.

Литература

• Дональд Кнут Искусство программирования, том 3. Сортировка и поиск
• Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Алгоритмы: построение и анализ

Ссылки

• Визуализатор 1 — Java-аплет.
• Визуализатор 2 — Java-аплет.