QpmtnriLmax — различия между версиями
(→Время работы) |
|||
| Строка 37: | Строка 37: | ||
Из-за максимального потока в расширенной сети могут быть рассчитаны в <tex>O (m n^3)</tex> шагов, возможность проверки может быть сделано с такой же сложности. Для решения задачи <tex>Q|pmtn; r_{i}|L_{max}</tex> мы используем бинарный поиск. Получается алгоритм со сложностью <tex>O (mn^3(log(n) + log (\max\limits_{i=1}^{n} p_i)) </tex>, потому что <tex>L_{max}</tex>, ограничен <tex>n \max\limits_{i=1}^{n}p_i</tex>, при <tex>s_1 = 1</tex>. | Из-за максимального потока в расширенной сети могут быть рассчитаны в <tex>O (m n^3)</tex> шагов, возможность проверки может быть сделано с такой же сложности. Для решения задачи <tex>Q|pmtn; r_{i}|L_{max}</tex> мы используем бинарный поиск. Получается алгоритм со сложностью <tex>O (mn^3(log(n) + log (\max\limits_{i=1}^{n} p_i)) </tex>, потому что <tex>L_{max}</tex>, ограничен <tex>n \max\limits_{i=1}^{n}p_i</tex>, при <tex>s_1 = 1</tex>. | ||
| − | <tex>Q | pmtn; ri | Cmax</tex> представляет собой частный случай <tex>Q | pmtn; ri | Lmax</tex>, и может быть решена более эффективно. Labetoulle, Lawler, Lenstra, | + | <tex>Q | pmtn; ri | Cmax</tex> представляет собой частный случай <tex>Q | pmtn; ri | Lmax</tex>, и может быть решена более эффективно. Labetoulle, Lawler, Lenstra, и Rinnooy Kan разработали алгоритм работающий за <tex> O(n log(n) + mn) </tex> специально для этого случая. |
{{Утверждение | {{Утверждение | ||
|statement= Задача <tex>Q | pmtn | Lmax</tex> может быть решена за <tex> O(n log(n) + mn) </tex> шагов. | |statement= Задача <tex>Q | pmtn | Lmax</tex> может быть решена за <tex> O(n log(n) + mn) </tex> шагов. | ||
Версия 21:21, 28 мая 2012
Постановка задачи
Рассмотрим задачу нахождения расписания со следующим свойством:
- Каждое задание имеет своё времени выпуска и срок завершения(дедлайн) .
Алгоритм решения
Применим бинарный поиск для общего решения задачи. Сведем задачу к поиску потока сети.
Пусть упорядоченная последовательности всех значений и .
Также определим для .
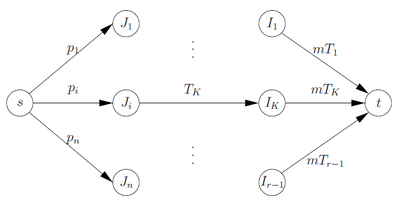
Далее мы расширяем сеть, показанную на рисунке 1 следующим образом:
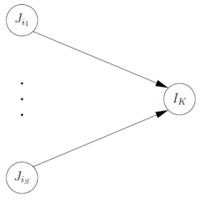
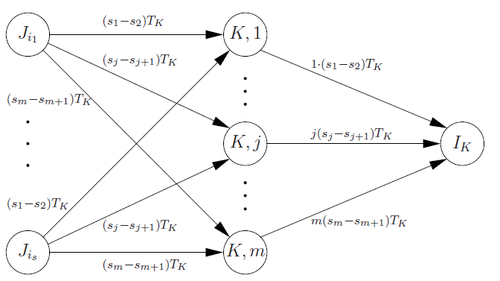
- произвольный интервал узел на рисунке, обозначим через набор предшественников узла . Тогда замененная нами подсеть определяется как , которая показана на рисунке 2.1; Расширение сети показано на рисунке 2.2.
Cчитаем, что машины индексируются в порядке невозрастания скоростей , кроме того .
Расширенная подсеть строится путем добавления к вершинам вершин . При , есть дуги от до с емкостью и для всех и существует дуга из в с емкостью .
Для каждого у нас есть такие расширения. Кроме того, мы сохраняем дуги из в емкостью и дуги из в емкостью (см. рисунок 1).
| Теорема: |
Следующие свойства эквивалентны:
(А) Существует допустимое расписание. (Б) В расширенной сети существует поток от s до t со значением |
Время работы
Из-за максимального потока в расширенной сети могут быть рассчитаны в шагов, возможность проверки может быть сделано с такой же сложности. Для решения задачи мы используем бинарный поиск. Получается алгоритм со сложностью , потому что , ограничен , при .
представляет собой частный случай , и может быть решена более эффективно. Labetoulle, Lawler, Lenstra, и Rinnooy Kan разработали алгоритм работающий за специально для этого случая.
| Утверждение: |
Задача может быть решена за шагов. |
|
Решение эквивалентно нахождению наименьшего , такого, что задача с "временными окнами" имеет решение. С другой стороны, решение эквивалентно нахождению такого наименьшего , такого, что задача с "временными окнами" или с "временными окнами" имеет решение. |
Таким образом, задачи и симметричны.