O2Cmax

Эта статья находится в разработке!

Постановка задачи

Рассмотрим задачу:

1. Дано [math]n[/math] работ и [math]2[/math] станка.
2. Для каждой работы известно её время выполнения на каждом станке.

Требуется минимизировать время окончания всех работ, если каждую работу необходимо выполнить на обоих станках.

Описание алгоритма

Пусть [math]a_{i}[/math] — время выполнения [math]i[/math]-ой работы на первом станке, а [math]b_{i}[/math] — на втором.

1. Разобьём все работы на два множества: [math]I = \{i \mid a_{i} \le b_{i}; i = 1, \dots, n\}[/math] и [math]J = \{i \mid a_{i} \gt b_{i}; i = 1, \dots, n\}[/math]
2. Найдем [math]a_{x} = \max \{a_{i} \mid i \in I\}[/math] и [math]b_{y} = \max \{b_{i} \mid i \in J\}[/math]
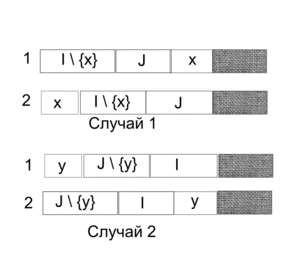
3. Рассмотрим 2 случая. Первый случай, когда [math]a_{x} \ge b_{y}[/math], тогда
   • Выполняем все работы на первом станке в следующем порядке: сперва все работы из [math]I \setminus \{x\}[/math], затем из [math]J[/math] и последней работу [math]x[/math]
   • На втором станке выполняем первой работу [math]x[/math]
   • Остальные работы выполняем на втором станке в порядке их завершения на первом тогда, когда второй станок свободен, а работа на первом уже выполнена

   Второй случай рассматривается аналогично: первый и второй станок меняются местами, и вместо [math]x[/math] — работа [math]y[/math]

Псевдокод

  [math]I \leftarrow \varnothing [/math]
  [math]J \leftarrow \varnothing [/math]
  for [math]i = 1 \dots n[/math]
     if [math]a_{i} \le b{i}[/math]
        [math] I \leftarrow I \cup \{i\} [/math]
     else
        [math] J \leftarrow J \cup \{i\} [/math]
  Найти [math]x[/math], где [math]a_{x} = \max \limits_{i \in I} \{a_{i}\}[/math]
  Найти [math]y[/math], где [math]b_{y} = \max \limits_{i \in J} \{b_{i}\}[/math]
  if [math]a_{x} \lt  b_{y}[/math]
     Поменять местами первый и второй станок
     Пересчитать [math]I, J, x[/math]
     Запомнить, что поменяли
  
  [math]time1 \leftarrow 0[/math]
  shed2[x] [math]\leftarrow 0[/math]
  [math]time2 \leftarrow b_{x}[/math]
  
  Для всех [math]i \in I \setminus \{x\}[/math]
     sched1[i] [math]\leftarrow time1[/math]
     [math]time1 \leftarrow time1 + a_{i}[/math]
     [math]time2 \leftarrow \max\{time1, time2\}[/math]
     sched2[i] [math]\leftarrow time2[/math]
     [math]time2 \leftarrow time2 + b_{i}[/math]
  
  Для всех [math]i \in J[/math]
     sched1[i] [math]\leftarrow time1[/math]
     [math]time1 \leftarrow time1 + a_{i}[/math]
     [math]time2 \leftarrow \max\{time1, time2\}[/math]
     sched2[i] [math]\leftarrow time2[/math]
     [math]time2 \leftarrow time2 + b_{i}[/math]
  
  [math]time1 \leftarrow \max\{time1, b_{x}\}[/math]
  sched1[x] [math]\leftarrow time1[/math]
  [math]time1 \leftarrow time1 + a_{x}[/math]
  
  [math]C_{max} \leftarrow \max\{time1, time2\}[/math]
  if станки меняли местами
     поменять их обратно

Сложность алгоритма

Каждое из множеств в сумме содержит [math]n[/math] элементов. Следовательно, чтобы найти максимум в каждом из множеств нам потребуется [math]O(n)[/math] операций, чтобы составить расписание для каждой работы из множества нам потребуется так же [math]O(n)[/math] операций. Получаем сложность алгоритма [math]O(n)[/math].