Дерево поиска, наивная реализация — различия между версиями
(сам поправил) |
Yulya3102 (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
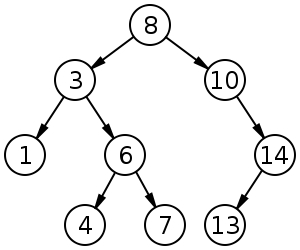
| − | [[Файл:Binary_search_tree.svg.png|right| | + | [[Файл:Binary_search_tree.svg.png|right|300px|thumb|Бинарное дерево поиска из 9 элементов]]'''Бинарное дерево поиска (англ. binary search tree, BST)''' - структура данных для работы с динамическими множествами. |
| − | Бинарное дерево поиска обладает следующим свойством: если <tex>x</tex> - узел бинарного дерева с ключом <tex>k</tex>, то все узлы в левом поддереве должны иметь ключи, меньшие | + | Бинарное дерево поиска обладает следующим свойством: если <tex>x</tex> - узел бинарного дерева с ключом <tex>k</tex>, то все узлы в левом поддереве должны иметь ключи, меньшие <tex>k</tex>, а в правом поддереве большие <tex>k</tex>. |
== Операции в бинарном дереве поиска == | == Операции в бинарном дереве поиска == | ||
=== Обход дерева поиска === | === Обход дерева поиска === | ||
Для вывода всех ключей бинарного дерева поиска в отсортированном порядке используется простой алгоритм (англ. ''inorder tree traversal''). | Для вывода всех ключей бинарного дерева поиска в отсортированном порядке используется простой алгоритм (англ. ''inorder tree traversal''). | ||
| − | + | inorderTreeWalk(Node x) | |
| − | if | + | if x != null |
| − | + | inorderTreeWalk(x.left) | |
| − | print(x.key) | + | print(x.key) |
| − | + | inorderTreeWalk(x.right) | |
Данный алгоритм выполняет обход за время <tex>O(n)</tex>, поскольку процедура вызывается ровно два раза для каждого узла дерева. Корректность данного алгоритма следует из свойств бинарного дерева поиска. | Данный алгоритм выполняет обход за время <tex>O(n)</tex>, поскольку процедура вызывается ровно два раза для каждого узла дерева. Корректность данного алгоритма следует из свойств бинарного дерева поиска. | ||
=== Поиск элемента === | === Поиск элемента === | ||
| − | [[Файл:Bst search.png|thumb| | + | [[Файл:Bst search.png|thumb|318px|Поиск элемента 4]] |
| − | Для поиска элемента в бинарном дереве поиска можно воспользоваться следующей процедурой. | + | Для поиска элемента в бинарном дереве поиска можно воспользоваться следующей процедурой, которая принимает в качестве параметров корень дерева и искомый ключ. Для каждого узла функция сравнивает значение его ключа с искомым ключом. Если ключи одинаковы, то функция возвращает текущий узел, в противном случае функция вызывается рекурсивно для левого или правого поддерева. Узлы, которые посещает функция образуют нисходящий путь от корня, так что время ее работы <tex>O(h)</tex>, где <tex>h</tex> - высота дерева. |
| − | + | treeSearch(Node x, key k) | |
| − | if | + | if x == null or k == x.key |
| − | return x | + | return x |
| − | if | + | if k < x.key |
| − | return | + | return treeSearch(x.left, k) |
else | else | ||
| − | return | + | return treeSearch(x.right, k) |
| − | + | ||
=== Поиск минимума и максимума === | === Поиск минимума и максимума === | ||
Чтобы найти минимальный элемент в бинарном дереве поиска, необходимо просто следовать указателям left от корня дерева, пока не встретится значение null. Если у вершины есть левое поддерево, то по свойству бинарного дерева поиска в нем хранятся все элементы с меньшим ключом. Если его нет, значит эта вершина и есть минимальная. Аналогично ищется и максимальный элемент. Для этого нужно следовать правым указателям. | Чтобы найти минимальный элемент в бинарном дереве поиска, необходимо просто следовать указателям left от корня дерева, пока не встретится значение null. Если у вершины есть левое поддерево, то по свойству бинарного дерева поиска в нем хранятся все элементы с меньшим ключом. Если его нет, значит эта вершина и есть минимальная. Аналогично ищется и максимальный элемент. Для этого нужно следовать правым указателям. | ||
| − | + | treeMinimum(Node x) | |
| − | while | + | while x.left != null |
| − | x = x.left | + | x = x.left |
| − | return x | + | return x |
| − | + | treeMaximum(Node x) | |
| − | while | + | while x.right != null |
| − | x = x.right | + | x = x.right |
| − | return x | + | return x |
Данные функции принимают корень дерева, и возвращают минимальный(максимальный) элемент в дереве. Обе процедуры выполняются за время <tex>O(h)</tex>. | Данные функции принимают корень дерева, и возвращают минимальный(максимальный) элемент в дереве. Обе процедуры выполняются за время <tex>O(h)</tex>. | ||
=== Поиск следующего и предыдущего элемента === | === Поиск следующего и предыдущего элемента === | ||
| − | + | Если у узла есть правое поддерево, то следующий за ним элемент будет минимальным элементом в этом поддереве. Если у него нет правого поддерева, то нужно следовать вверх, пока не встретим узел, который является левым дочерним узлом своего родителя. Поиск предыдущего выполнятся аналогично. Если у узла есть левое поддерево, то следующий за ним элемент будет максимальным элементом в этом поддереве. Если у него нет левого поддерева, то нужно следовать вверх, пока не встретим узел, который является правым дочерним узлом своего родителя. | |
| − | if | + | treeNext(Node x) |
| − | return | + | if x.right != null |
| − | y = x.parent | + | return treeMinimum(x.right) |
| − | while | + | y = x.parent |
| − | x = y | + | while y != null and x == y.right |
| − | y = y.parent | + | x = y |
| − | return y | + | y = y.parent |
| + | return y | ||
| − | + | treePrev(Node x) | |
| − | if | + | if x.left != null |
| − | return | + | return treeMaximum(x.left) |
| − | y = x.parent | + | y = x.parent |
| − | while | + | while y != null and x == y.left |
| − | x = y | + | x = y |
| − | y = y.parent | + | y = y.parent |
| − | return y | + | return y |
| − | + | Обе операции выполняются за время <tex>O(h)</tex>. | |
=== Вставка === | === Вставка === | ||
Операция вставки работает аналогично поиску элемента, только при обнаружении нулевого указателя нужно подвесить на него вставляемый элемент. Приведем итеративную реализацию этого алгоритма. | Операция вставки работает аналогично поиску элемента, только при обнаружении нулевого указателя нужно подвесить на него вставляемый элемент. Приведем итеративную реализацию этого алгоритма. | ||
| − | + | treeInsert(Node x, Node z) // корень дерева, вставляемый элемент | |
| − | + | Node y = null | |
| − | while | + | while x != null |
| − | y = x | + | y = x |
| − | if | + | if z.key > x.key |
| − | x = x.right | + | x = x.right |
else | else | ||
| − | x = x.left | + | x = x.left |
| − | z.parent = y | + | z.parent = y |
| − | if | + | if z.key > y.key |
| − | y.right = z | + | y.right = z |
else | else | ||
| − | y.left = z | + | y.left = z |
Время работы алгоритма <tex>O(h)</tex>. | Время работы алгоритма <tex>O(h)</tex>. | ||
=== Удаление === | === Удаление === | ||
| Строка 76: | Строка 77: | ||
|- | |- | ||
|'''Удаление листа''' | |'''Удаление листа''' | ||
| − | | [[Файл:Bst_del1.png | + | | [[Файл:Bst_del1.png]] |
|- | |- | ||
|'''Удаление узла с одним дочерним узлом''' | |'''Удаление узла с одним дочерним узлом''' | ||
| − | | [[Файл:Bst_del2.png | + | | [[Файл:Bst_del2.png]] |
|- | |- | ||
|'''Удаление узла с двумя дочерними узлами''' | |'''Удаление узла с двумя дочерними узлами''' | ||
| − | | [[Файл:Bst_del3.png | + | | [[Файл:Bst_del3.png]] |
|- | |- | ||
|'''Удаление корня''' | |'''Удаление корня''' | ||
| − | | [[Файл:Bst_del4.png | + | | [[Файл:Bst_del4.png]] |
|} | |} | ||
| − | + | treeDelete(Node t, Node z) // корень дерева, удаляемый элемент | |
| − | + | Node x, y | |
| − | if | + | if z.left == null or z.right == null |
| − | y = z | + | y = z |
else | else | ||
| − | y = | + | y = treeNext(z) |
| − | if | + | if y.left != null |
| − | x = y.left | + | x = y.left |
else | else | ||
| − | x = y.right | + | x = y.right |
| − | if | + | if x != null |
| − | x.parent = y.parent | + | x.parent = y.parent |
| − | if | + | if y.parent == null |
| − | t = x | + | t = x |
else | else | ||
| − | if | + | if y == y.parent.left |
| − | y.parent.left = x | + | y.parent.left = x |
else | else | ||
| − | y.parent.right = x | + | y.parent.right = x |
| − | + | if y != z | |
| − | + | z.key = y.key | |
| − | + | z.data = y.data | |
| − | + | return y | |
== Литература == | == Литература == | ||
Версия 16:27, 9 июня 2012
Бинарное дерево поиска обладает следующим свойством: если - узел бинарного дерева с ключом , то все узлы в левом поддереве должны иметь ключи, меньшие , а в правом поддереве большие .
Содержание
Операции в бинарном дереве поиска
Обход дерева поиска
Для вывода всех ключей бинарного дерева поиска в отсортированном порядке используется простой алгоритм (англ. inorder tree traversal).
inorderTreeWalk(Node x)
if x != null
inorderTreeWalk(x.left)
print(x.key)
inorderTreeWalk(x.right)
Данный алгоритм выполняет обход за время , поскольку процедура вызывается ровно два раза для каждого узла дерева. Корректность данного алгоритма следует из свойств бинарного дерева поиска.
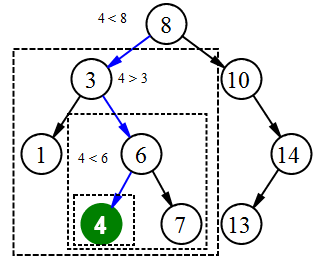
Поиск элемента
Для поиска элемента в бинарном дереве поиска можно воспользоваться следующей процедурой, которая принимает в качестве параметров корень дерева и искомый ключ. Для каждого узла функция сравнивает значение его ключа с искомым ключом. Если ключи одинаковы, то функция возвращает текущий узел, в противном случае функция вызывается рекурсивно для левого или правого поддерева. Узлы, которые посещает функция образуют нисходящий путь от корня, так что время ее работы , где - высота дерева.
treeSearch(Node x, key k)
if x == null or k == x.key
return x
if k < x.key
return treeSearch(x.left, k)
else
return treeSearch(x.right, k)
Поиск минимума и максимума
Чтобы найти минимальный элемент в бинарном дереве поиска, необходимо просто следовать указателям left от корня дерева, пока не встретится значение null. Если у вершины есть левое поддерево, то по свойству бинарного дерева поиска в нем хранятся все элементы с меньшим ключом. Если его нет, значит эта вершина и есть минимальная. Аналогично ищется и максимальный элемент. Для этого нужно следовать правым указателям.
treeMinimum(Node x)
while x.left != null
x = x.left
return x
treeMaximum(Node x)
while x.right != null
x = x.right
return x
Данные функции принимают корень дерева, и возвращают минимальный(максимальный) элемент в дереве. Обе процедуры выполняются за время .
Поиск следующего и предыдущего элемента
Если у узла есть правое поддерево, то следующий за ним элемент будет минимальным элементом в этом поддереве. Если у него нет правого поддерева, то нужно следовать вверх, пока не встретим узел, который является левым дочерним узлом своего родителя. Поиск предыдущего выполнятся аналогично. Если у узла есть левое поддерево, то следующий за ним элемент будет максимальным элементом в этом поддереве. Если у него нет левого поддерева, то нужно следовать вверх, пока не встретим узел, который является правым дочерним узлом своего родителя.
treeNext(Node x)
if x.right != null
return treeMinimum(x.right)
y = x.parent
while y != null and x == y.right
x = y
y = y.parent
return y
treePrev(Node x)
if x.left != null
return treeMaximum(x.left)
y = x.parent
while y != null and x == y.left
x = y
y = y.parent
return y
Обе операции выполняются за время .
Вставка
Операция вставки работает аналогично поиску элемента, только при обнаружении нулевого указателя нужно подвесить на него вставляемый элемент. Приведем итеративную реализацию этого алгоритма.
treeInsert(Node x, Node z) // корень дерева, вставляемый элемент
Node y = null
while x != null
y = x
if z.key > x.key
x = x.right
else
x = x.left
z.parent = y
if z.key > y.key
y.right = z
else
y.left = z
Время работы алгоритма .
Удаление
Для удаления узла из бинарного дерева поиска нужно рассмотреть три возможные ситуации. Если у узла нет дочерних узлов, то у его родителя нужно просто заменить указатель на null. Если у узла есть только один дочерний узел, то нужно создать новую связь между родителем удаляемого узла и его дочерним узлом. Наконец, если у узла два дочерних узла, то нужно найти следующий за ним элемент(у этого элемента не будет левого потомка) и переместить его на место удаляемого узла. Время работы алгоритма .
| Случай | Иллюстрация |
|---|---|
| Удаление листа | 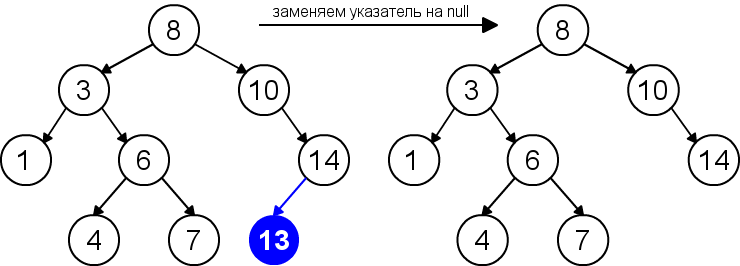
|
| Удаление узла с одним дочерним узлом | 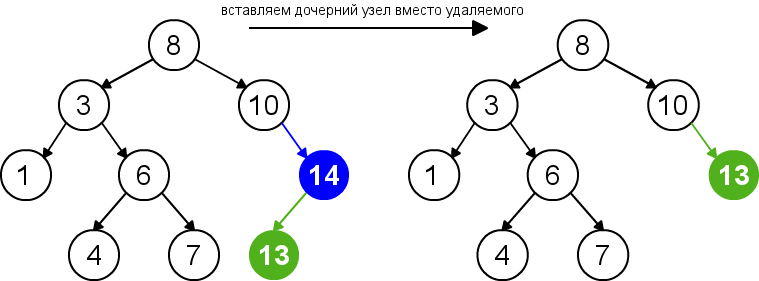
|
| Удаление узла с двумя дочерними узлами | 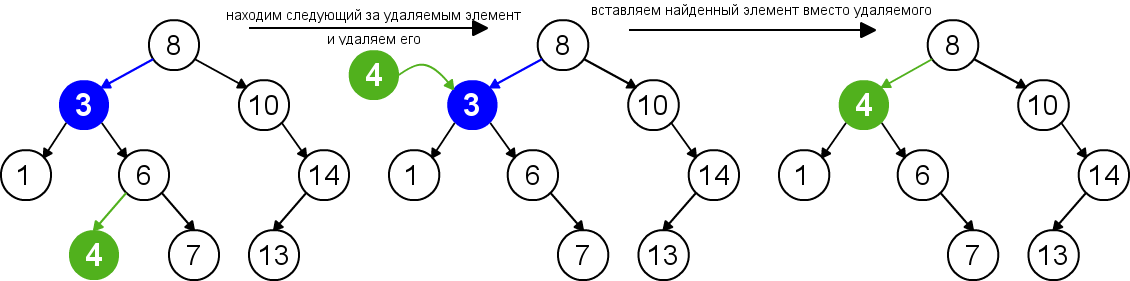
|
| Удаление корня | 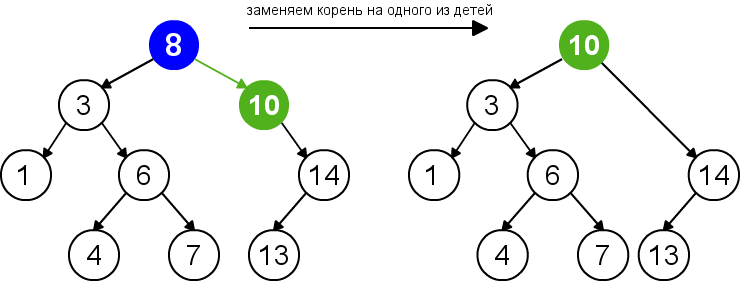
|
treeDelete(Node t, Node z) // корень дерева, удаляемый элемент
Node x, y
if z.left == null or z.right == null
y = z
else
y = treeNext(z)
if y.left != null
x = y.left
else
x = y.right
if x != null
x.parent = y.parent
if y.parent == null
t = x
else
if y == y.parent.left
y.parent.left = x
else
y.parent.right = x
if y != z
z.key = y.key
z.data = y.data
return y
Литература
1. Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Алгоритмы: построение и анализ = Introduction to Algorithms / Под ред. И. В. Красикова. — 2-е изд. — М.: Вильямс, 2005. — 1296 с. — ISBN 5-8459-0857-4