Целочисленный двоичный поиск — различия между версиями
(→Код) |
(→Код) |
||
| Строка 27: | Строка 27: | ||
== Код == | == Код == | ||
| − | <pre> l | + | <pre>BinSearch(l, r) // l, r - левая и правая границы |
| − | + | while l < r - 1 // запускаем цикл | |
| − | + | m = (l + r) / 2; // m - середина области поиска | |
| − | + | if a[m] < k | |
| − | + | l = m; | |
| − | + | else | |
| − | + | r = m; // сужение границ | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</pre> | </pre> | ||
В случае правостороннего поиска изменится знак сравнения при сужении границ на (a[m] <= k), также при выводе найденного индекса, мы сравниваем искомый элемент k с a[l]. | В случае правостороннего поиска изменится знак сравнения при сужении границ на (a[m] <= k), также при выводе найденного индекса, мы сравниваем искомый элемент k с a[l]. | ||
Версия 23:49, 11 июня 2012
| Определение: |
| Целочисленный двоичный поиск (бин. поиск) - алгоритм поиска объекта по заданному признаку во множестве объектов, упорядоченных по тому же самому признаку. |
Содержание
Формулировка задачи
Пусть нам дан упорядоченный массив, состоящий только из целочисленых элементов. Нам надо найти в нем индекс, по которому находиться искомый элемент, или же мы можем находить интервалы вхождения искомого элемента. Для этой задачи мы и можем использовать двоичный поиск.
Принцип работы
Двоичный поиск заключается в том, что на каждом шаге множество объектов делится на две части и в работе остается та часть множества, где находится искомый объект. Или же, в зависимости от постоновки задачи, мы можем остановить процесс, когда мы получим первый или же последний индекс вхождения элемента. Последнее условие - это левосторонний/правосторонний двоичный поиск.
Правосторонний/левосторонний целочисленный двоичный поиск
Когда мы ищем правосторонним бин. поиском, то он возвращает индекс самого правого вхождения заданного значения х.
Когда же поиск левосторонний, возвращается индекс самого левого вхождения заданного значения х.
Это разделение помогает находить количество подряд идущих равных значений.
Например:
Задан отсортированный массив [1, 2, 2, 2, 2, 3, 5, 8, 9, 11]
Правосторонний поиск двойки выдаст в результате 5, в то время как левосторонний выдаст 2.
От сюда следует, что количество подряд идущих двоек равно длине отрезка [2;5] = 4.
Если искомого элемента нету, то правосторонний поиск выдаст минимальный элемент, больший искомого, а левосторонний наоборот, максимальный элемент, меньший искомого.
Алгоритм правостороннего/левостороннего поиска
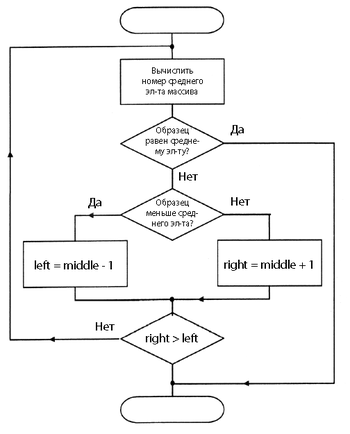
Идея поиска заключается в том, чтобы брать элемент посередине, между границами, и сравнивать его с искомым. В случае равенства возвращать его, а если искомое больше(в случае правостороннего - не меньше), чем элемент сравнения, то сужаем область поиска так, чтобы новая левая граница была равна индексу середины предыдущей области. В противном случае присваиваем это значение правой границе. Проделываем эту процедуру до тех пор, пока правая граница больше левой более чем на 1, или же пока мы не найдём искомый индекс.
Код
BinSearch(l, r) // l, r - левая и правая границы
while l < r - 1 // запускаем цикл
m = (l + r) / 2; // m - середина области поиска
if a[m] < k
l = m;
else
r = m; // сужение границ
В случае правостороннего поиска изменится знак сравнения при сужении границ на (a[m] <= k), также при выводе найденного индекса, мы сравниваем искомый элемент k с a[l].
Инвариант цикла: l <= r && «если k == a[k], то l <= k <= r»
Источники
- Д. Кнут - Искусство программирования (Том 3, 2-е издание)