Эволюционные алгоритмы многокритериальной оптимизации, основанные на индикаторах. Гиперобъем — различия между версиями
(Новая страница: «{{В разработке}} Существует много различных индикаторов, с помощью которых численно оцен...») |
Fkorotkov (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
{{В разработке}} | {{В разработке}} | ||
| + | |||
| + | {{Определение | ||
| + | |definition=Задача многокритериальной оптимизации формулируется следующим образом: | ||
| + | <tex>\mathrm{maximize f(x)=(f_1(x), f_2(x),\ldots,f_d(x))}</tex>, где <tex>\mathrm{f(x):X \rightarrow R^d}</tex> (<tex>d</tex> - количество критериев). | ||
| + | }} | ||
| + | |||
| + | Надо заметить, что под термином <tex>maximize</tex> мы понимаем оптимальность по Парето. | ||
| + | {{Определение | ||
| + | |definition=Множество <tex>X^* \subseteq X</tex> называется Парето оптимальным, если: | ||
| + | <tex>\mathrm{\forall x^* \subset X^* \not \exists x \subset X : x \succ x^*}</tex>, | ||
| + | где <tex>\left(x \succ x^* \leftrightarrow \forall i \in 1 \ldots d: \left( f_i(x) \geq f_i(x^*)\right)\right) \bigwedge \left( \exists i \in 1 \ldots d: \left( f_i(x) \geq f_i(x^*)\right)\right) </tex> | ||
| + | }} | ||
Существует много различных индикаторов, с помощью которых численно оценивают качество множества решений. Но широко используется только один. | Существует много различных индикаторов, с помощью которых численно оценивают качество множества решений. Но широко используется только один. | ||
| Строка 14: | Строка 26: | ||
Пример: | Пример: | ||
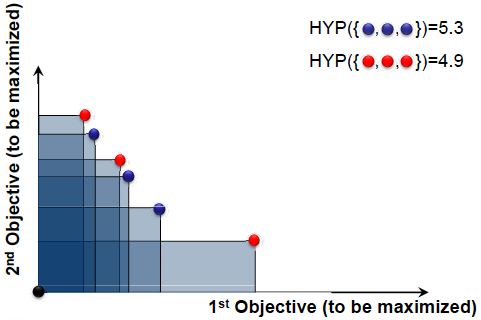
Пусть <tex>\mathrm{r = \left(0, 0, \ldots, 0 \right)}</tex> и <tex>d=2</tex>. Тогда гиперобъем - это площадь объединения прямоугольников(см. рис). | Пусть <tex>\mathrm{r = \left(0, 0, \ldots, 0 \right)}</tex> и <tex>d=2</tex>. Тогда гиперобъем - это площадь объединения прямоугольников(см. рис). | ||
| + | [[File:Chart.png]] | ||
Версия 22:44, 17 июня 2012
Эта статья находится в разработке!
| Определение: |
| Задача многокритериальной оптимизации формулируется следующим образом: , где ( - количество критериев). |
Надо заметить, что под термином мы понимаем оптимальность по Парето.
| Определение: |
| Множество называется Парето оптимальным, если:
, где |
Существует много различных индикаторов, с помощью которых численно оценивают качество множества решений. Но широко используется только один.
| Определение: |
| Индикатор называется эластичным по Паретто(Pareto-compliant), если для любых двух множест решения и значение индикатора для больше значения для тогда и только тогда, когда доминирует . |
Дадим определение индикатора гиперобъема.
| Определение: |
| Пусть дано множество решения . Пусть также множество всех решений усечено некоторой точкой . Тогда: , где через обозначена мера множества по Лебегу. |
Пример:
Пусть и . Тогда гиперобъем - это площадь объединения прямоугольников(см. рис).