O2Cmax — различия между версиями
Dimitrova (обсуждение | вклад) |
Dimitrova (обсуждение | вклад) (→Доказательство корректности алгоритма) |
||
| Строка 24: | Строка 24: | ||
==Доказательство корректности алгоритма== | ==Доказательство корректности алгоритма== | ||
| + | {{Теорема | ||
| + | |statement= | ||
| + | Расписание, построенное данным алгоритмом, является корректным и оптимальным. | ||
| + | |proof= | ||
Для доказательства оптимальности полученного расписания рассмотрим только первый случай. Второй доказывается аналогично. | Для доказательства оптимальности полученного расписания рассмотрим только первый случай. Второй доказывается аналогично. | ||
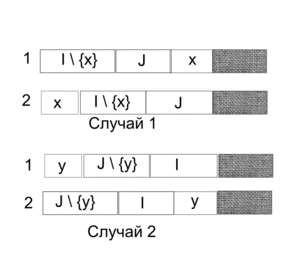
Рассмотрим 3 последовательности выполнения работы, начиная с нулевого времени: все работы на первом станке, все работы на втором станке и первая работа на втором станке плюс последняя - на первом.<br/> | Рассмотрим 3 последовательности выполнения работы, начиная с нулевого времени: все работы на первом станке, все работы на втором станке и первая работа на втором станке плюс последняя - на первом.<br/> | ||
| Строка 45: | Строка 49: | ||
</ol> | </ol> | ||
Три последовательности выполнения работ, которые мы рассмотрели вначале, являются нижней оценкой для OpenShop problem, следовательно они и дают оптимальное решение. | Три последовательности выполнения работ, которые мы рассмотрели вначале, являются нижней оценкой для OpenShop problem, следовательно они и дают оптимальное решение. | ||
| + | }} | ||
==Псевдокод== | ==Псевдокод== | ||
Версия 21:53, 18 июня 2012
Содержание
Постановка задачи
Рассмотрим задачу:
- Дано работ и станка.
- Для каждой работы известно её время выполнения на каждом станке.
Требуется минимизировать время окончания всех работ, если каждую работу необходимо выполнить на обоих станках.
Описание алгоритма
Пусть — время выполнения -ой работы на первом станке, а — на втором.
- Разобьём все работы на два множества: и
- Найдем и
- Рассмотрим 2 случая. Первый случай, когда , тогда
- Выполняем все работы на первом станке в следующем порядке: сперва все работы из , затем из и последней работу
- На втором станке выполняем первой работу
- Остальные работы выполняем на втором станке в порядке их завершения на первом тогда, когда второй станок свободен, а работа на первом уже выполнена
Второй случай рассматривается аналогично: первый и второй станок меняются местами, и вместо — работа
Доказательство корректности алгоритма
| Теорема: |
Расписание, построенное данным алгоритмом, является корректным и оптимальным. |
| Доказательство: |
|
Для доказательства оптимальности полученного расписания рассмотрим только первый случай. Второй доказывается аналогично.
Рассмотрим 3 последовательности выполнения работы, начиная с нулевого времени: все работы на первом станке, все работы на втором станке и первая работа на втором станке плюс последняя - на первом.
|
Псевдокод
for if else Найти , где Найти , где if Поменять местами первый и второй станок Пересчитать Запомнить, что поменяли shed2[x] Для всех sched1[i] sched2[i] Для всех sched1[i] sched2[i] sched1[x] if станки меняли местами поменять их обратно
Сложность алгоритма
Каждое из множеств в сумме содержит элементов. Следовательно, чтобы найти максимум в каждом из множеств нам потребуется операций, чтобы составить расписание для каждой работы из множества нам потребуется так же операций. Получаем сложность алгоритма .