Связь между максимизацией гиперобъема и аппроксимацией Парето-фронта

Основные определения

Определение:

Множество [math]X^* \subseteq \mathbb{X}[/math] называется Парето оптимальным, если: [math]\mathrm{\forall x^* \subset X^* \not \exists x \subset \mathbb{X : x \succ x^*}[/math], где [math] x \succ x^* [/math]([math]x[/math] доминирует [math]x^*[/math])[math] \leftrightarrow \left( \forall i \in 1 \ldots d: f_i(x) \geq f_i(x^*) \right) \bigwedge \left( \exists i \in 1 \ldots d: f_i(x) \gt f_i(x^*)\right)[/math] [math]P(X^*)[/math] - множество оптимальных по Парето решений, его также называют Парето-фронтом. Парето-фронт не может быть вычислен за полиномиальное время.

Определение:

Пусть [math]f \in \mathbb{F}, n \geq 3[/math] и [math]X = \{x_1, \ldots, x_n\} \in \mathbb{X}[/math]. Наименьшим вкладом этого множества называется [math]MinCon(X)= \min \limits_{2 \leq i \leq n-1} (x_i-x_{i-1})(f(x_i)- f(x_{i-1}))[/math].

Связь между максимизацией гиперобъема и аппроксимацией Парето-фронта

Множество функций вида: [math]f:[a,A] \rightarrow [b,B][/math], где [math]f[/math] убывает и [math]f(a)=B, f(A)=b[/math] обозначим через [math]\mathbb{F}[/math]. Коэффициент апроксимации монотонно убывающих функций не зависит от масштабов отрезков [math] [a,A][/math] и [math][b,B] [/math]. Так как для фиксированных констант [math] \mu , \nu [/math] функция [math] f^*:[ \mu a , \mu A ] \rightarrow [ \nu b , \nu B ][/math] и [math] f^*= \nu f(x/ \mu ) [/math] имеет тот же коэффициент аппроксимации. Однако, коэффициент аппроксимации зависит от значений [math]A/a[/math] и [math]B/b[/math].

Далее будем рассматривать только монотонно убывающие, полунепрерывные Парето-фронты. Условие полунепрерывности необходимо для того, чтобы существовало множество решение, максимизирующее индикатор гиперобъема.

Рассмотрим оптимальный коэффициент апроксимации для данного Парето-фронта из n ([math] \alpha _{OPT}[/math]) и верхнюю границу коэффициента аппроксимации для множества из n точек, максимизирующего значение индикатора гиперобъема ([math] \alpha _{HYP}[/math]) и докажем, что для количества точек [math] n [/math] они одинаковы, а именно [math] 1 + \Theta ( \frac{1}{n}) [/math].

Индикатор гиперобъема

Утверждение:

Пусть [math]f \in \mathbb{F}, n \in \mathbb{N}[/math]. Тогда существует, не обязятельно единственное, множество решения [math]X \in \mathbb{X}[/math], которое максимизирует значение гиперобъема ([math]HYP(X)[/math]) на [math]\mathbb{X}[/math]

[math]\triangleright[/math]

Доказательство представлено в статье Эволюционные алгоритмы многокритериальной оптимизации, основанные на индикаторах. Гиперобъем#Индикатор Гиперобъема

[math]\triangleleft[/math]

Нахождение лучшего коэффициента аппроксимации

Утверждение(3) ограничивает значение оптимального коэффицента апроксимации сверху: [math]1 + \frac{\log (\min ( \frac{A}{a}, \frac{B}{b}))}{n}[/math] = [math] 1 + \Theta ( \frac{1}{n}) [/math].

Нахождение коэффициента аппроксимации множества решения максимизируюшего гиперобъем

Утверждение:

Пусть [math]f \in \mathbb{F}, n \geq 3[/math] и [math]X= \{x_1, x_2, \ldots, x_d \} \in X [/math]. Тогда [MINCON] данного множество решения: [math]MINCON(X) \leq \frac{(x_n - x_1)(f(x_1) - f(x_n))}{(n-2)^2}[/math]

[math]\triangleright[/math]

Исходя из определения минимальный вклад в гиперобъем множества равен минимуму из всевозможных площадей прямоугольников, образующихся между соседними точками множества решения и их значениями. Пусть [math]a_i, b_i[/math] - длины сторон соответствующего прямоугольника, тогда: [math] a_i \geq MINCON(X)/b_i[/math], для любого [math]2 \leq i \leq n - 1[/math] Это означает: [math] \sum\limits_{i=2}^{n-1} MINCON(x)/b_i \leq \sum\limits_{i=2}^{n-1} a_i \leq \sum\limits_{i=2}^{n} a_i = \sum\limits_{i=2}^{n} x_i - \sum\limits_{i=1}^{n-1} x_i = x_n - x_1 [/math] и поэтому: [math]MINCON(X) \leq \frac{(x_n - x_1)}{\sum\limits_{i=2}^{n-1}1/b_i}[/math] Так как среднее гармоническое не больше среднего арифметического: [math] \frac{n - 2}{\sum\limits_{i=2}^{n-1}1/b_i} \leq \frac{\sum\limits_{i=2}^{n-1}1/b_i}{n - 2}[/math] Преобразуя, получаем искомое.

[math]\triangleleft[/math]

Далее необходимо посчитать коэффициент аппроксимации для "внутренних" ([math]x \in [x_1, x_n][/math]) и "внешних" точек ([math]x \lt x_1[/math] или [math]x \gt x_n[/math]).

Теорема (1):

Пусть [math]f \in \mathbb{F}, n \gt 4[/math]. Любое множество решение [math]\{x_1, x_2, \ldots, x_d\} \in X_{HYP}^f [/math] достигает [math]1 + \frac{ \sqrt{A/a} + \sqrt{B/b} }{n - 4}[/math] мультипликативной аппроксимации всех внутренних точек.

Доказательство:

[math]\triangleright[/math]

Доказательство производится от противного, принимая предположение, что существует такой [math] x[/math], для которого бы не выполнялось условие аппроксимации при данном коэффициенте.

[math]\triangleleft[/math]

Теорема (2):

Пусть [math]f \in \mathbb{F}, n \gt 3[/math]. И [math] R = (R_x, R_y) \leq (0, 0) [/math] является точкой отсчета. Каждое множество решение [math]\{x_1, x_2, \ldots, x_d\} \in X_{HYP}^f [/math] достигает [math]1 + \frac{A}{(a - R_x)(n - 2)^2}[/math] мультипликативной аппроксимации всех точек с [math]x \lt x_1[/math], и достигает [math]1 + \frac{B}{(b - R_y)(n - 2)^2}[/math] мультипликативной аппроксимации всех точек с [math]x \gt x_n[/math].

Доказательство:

[math]\triangleright[/math]

Доказательство производится c использованием ранее доказанного утверждения о MINCON.

[math]\triangleleft[/math]

Совместно теорема(1) и теорема(2) приводят к следующим следствиям:

Следствие 1: [math]\alpha_{opt} = 1 + \Theta(1/n)[/math]

Пусть [math]f \in \mathbb{F}, n \gt 4[/math], и [math] R = (R_x, R_y) \leq (0, 0) [/math] является точкой отсчета. Тогда:

[math] \lambda_{HYP} \leq 1 + \max{ \frac{ \sqrt{A/a} + \sqrt{B/b} }{n - 4}}{\frac{A}{(a - R_x)(n - 2)^2}}{\frac{B}{(b - R_y)(n - 2)^2}}[/math]

Следствие 2: [math]\alpha_{opt} = 1 + \Theta(1/n)[/math]

Пусть [math]f \in \mathbb{F}, n \gt 4[/math]. И [math] R = (R_x, R_y) \leq (0, 0) [/math] является точкой отсчета. Тогда если

[math] n \geq 2 + \max{\sqrt{A/a}}{\sqrt{B/b}}[/math]

или

[math]R_x \leq - \sqrt{Aa}/n, R_y \leq - \sqrt{Bb}/n[/math], выполняется следующее неравенство

[math] \alpha _{HYP} \leq 1 + \frac{ \sqrt{ \frac{A}{a}} + \sqrt{ \frac{B}{b}}}{n - 4}[/math] = [math] 1 + \Theta ( \frac{1}{n}) [/math],

то есть

[math] \alpha _{HYP} [/math] = [math] 1 + \Theta ( \frac{1}{n}) [/math],

что и требовалось доказать.

Утверждение (5):

Пусть [math]f \in \mathbb{F}, n \geq 3[/math] и [math]X = \{x_1, \ldots, x_n\} \in \mathbb{X}[/math], тогда [math]MinCon(X) \leq \frac{(x_n-x_1)(f(x_1)-f(x_n))}{(n-2)^2}[/math].

[math]\triangleright[/math]

Пусть [math]a_i=x_i-x_{i-1}[/math] [math]\forall i \in [2,n][/math] и [math]b_i=f(x_i)-f(x_{i-1})[/math] [math]\forall i \in [1,n-1][/math]. Подставив в определение(6), получим: [math]MinCon(X)= \min \limits_{2 \leq i \leq n-1} a_i b_i \Leftrightarrow a_i \geq MinCon(X) / b_i \forall i \in [2, n-1][/math] [math]\sum \limits_{i=2}^{n-1} MinCon(X) / b_i \leq \sum \limits_{i=2}^{n-1} a_i \leq \sum \limits_{i=2}^{n} a_i = \sum \limits_{i=2}^{n}x_i - \sum \limits_{i=1}^{n-1}x_i=x_n-x_1 [/math] Тогда [math]MinCon(X) \leq \frac{x_n-x_1}{\sum \limits_{i=2}^{n-1}1/b_i}[/math]. Cреднее гармоническое меньше среднего арифметического, поэтому [math]MinCon(X) \leq \frac{x_n-x_1}{\sum \limits_{i=2}^{n-1}1/b_i} \leq \frac{(x_n-x_1)\sum \limits_{i=2}^{n-1}b_i}{(n-2)^2} \leq \frac{(x_n-x_1)(f(x_1)-f(x_n))}{(n-2)^2}[/math].

[math]\triangleleft[/math]

Теорема:

Пусть [math]f \in \mathbb{F}, n \gt 4[/math] и [math]X = \{ x_1, \ldots, x_n \} \in \mathbb{X}[/math]. Тогда [math]\alpha = 1 + \frac{\sqrt{A/a} + \sqrt{B/b}}{n-4}[/math].

Доказательство:

[math]\triangleright[/math]

Допустим, что существует [math]x[/math], который не аппроксимируется [math]\alpha = 1 + \frac{\sqrt{A/a} + \sqrt{B/b}}{n-4}[/math]. Пусть [math]x_i \lt x \lt x_i+1[/math], тогда [math]x \gt \alpha x_i, f(x) \gt \alpha f(x_{i+1})[/math]. Известно, что [math]MinCon(X) \geq (x-x_i)(f(x)-f(x_{i+1}))[/math]. После подстановки получим [math]MinCon(X) \gt (\alpha - 1)^2 x_i f(x_{i+1})[/math] (1). Применив утверждение(5), получим: [math]\forall i \in [3, n-1][/math] [math]MinCon(X) \leq (x_i-x_1)(f(x_1)-f(x_i))/(i-2)^2 \leq x_iB/(i-2)^2[/math] (2) [math]\forall i \in [1, n-3][/math] [math]MinCon(X) \leq (x_n-x_{i+1})(f(x_{i+1})-f(x_n))/(n-i-2)^2 \leq A f(x_{i+1})/(n-i-2)^2[/math] (3) Таким образом, [math](\alpha - 1)^2 x_i f(x_{i+1}) \lt \min \{\frac{x_iB}{(i-2)^2} ,\frac{A f(x_{i+1})}{(n-i-2)^2}\} \Leftrightarrow[/math] [math]\alpha \lt 1 + \min \{\frac{\sqrt{x_iB}}{i-2} ,\frac{\sqrt{A f(x_{i+1})}}{n-i-2}\}[/math]. Т.к. [math]\frac{\sqrt{x_iB}}{i-2}[/math] монотонно убывает, а [math]\frac{\sqrt{A f(x_{i+1})}}{n-i-2}\}[/math] монотонно возрастает, то максимальное значение [math]\min \{\frac{\sqrt{x_iB}}{i-2} ,\frac{\sqrt{A f(x_{i+1})}}{n-i-2}\}[/math] достигается при равенстве обоих членов: [math]\frac{\sqrt{x_iB}}{i-2} = \frac{\sqrt{A f(x_{i+1})}}{n-i-2}\} \Leftrightarrow i = 2 + \frac{(n-4)\sqrt{B/b}}{\sqrt{A/a} + \sqrt{B/b}}[/math]. Получим верхнюю оценку для [math]\alpha[/math]: [math]\alpha \lt 1 + \frac{\sqrt{A/a} + \sqrt{B/b}}{n-4}[/math]. Вышесказанное верно для [math]3 \leq i \leq n-3[/math]. Для [math]i = 1, 2[/math] из (1) и (3) следует, что [math]\alpha \lt 1 + \frac{\sqrt{A/a}}{n-i-2} \leq 1 + \frac{\sqrt{A/a}}{n-4}[/math], что невозможно по условию теоремы. Для [math]i = n-2, n-1[/math] по (1) и (2) [math]\alpha \lt 1 + \frac{ \sqrt{B/b} } {i-2} \leq 1 + \frac {\sqrt {B/b} } {n-4}[/math], что тоже невозможно по условию теоремы.

[math]\triangleleft[/math]

Примечание

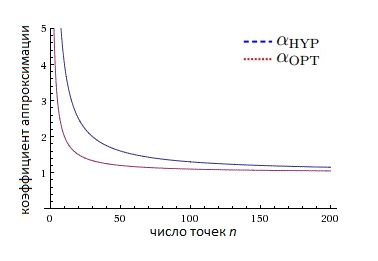
Конечно, зависимость от [math] [a,A][/math] и [math][b,B] [/math] в аппроксимационном коэффициенте оптимального множества решения меньше чем в аппроксимационном коэффициенте для множества, максимизирующего гиперобъем. Однако, полученная граница для коэффициента аппроксимации является верхней. На рисунке ниже можно увидеть пример поведения данных значений для определенного класса функций.

Источники

1. Friedrich T., Bringmann K. - The Maximum Hypervolume Set Yields Near-optimal Approximation