Задача многокритериальной оптимизации. Multiobjectivization — различия между версиями

Материал из Викиконспекты
Перейти к: навигация, поиск
(→‎Введение)
(→‎Задачи)
Строка 70: Строка 70:
  
 
== Задачи ==
 
== Задачи ==
 +
====Hierarchical-if-and-only-if function====
 +
'''H-IIF''' – предназначена для моделирования проблемы с блочной структурой, каждый блок которой строго связан с остальными блоками.
 +
 +
 +
:<math>
 +
f(B)= \begin{cases}1,& \mbox{if } |B| = 1, \mbox{ else}
 +
\\|B|+f(B_L)+f(B_R),& \mbox{if }(\forall i \{b_i=0\} \mbox{ or } \forall i \{b_i = 1 \})
 +
\\f(B_L) + f(B_R), & \mbox{otherwise}
 +
\end{cases}
 +
</math>,
 +
 +
где <math>B</math> &ndash; блок бит <math>\{b_1,b_2,\dots,b_n \}, |B|</math> &ndash; размер блока, а <math>B_L, B_R</math> &ndash; левая и правая часть блока соответственно.
 +
 +
Применяя к этой задаче мультиобъективизацию, разобьём задачу <math>f</math> на <math>k</math>-задач.
 +
 +
Представим, как будет выглядеть <math>f(B)</math>:
 +
 +
:<math>
 +
f(B)= \begin{cases}
 +
0, & \mbox{if } |B| = 1 \mbox{ and }b_1 \neq k,  \mbox{ else}
 +
\\1,& \mbox{if } |B| = 1 \mbox{ and }b_1 = k,  \mbox{ else}
 +
\\|B|+f_k(B_L)+f_k(B_R),& \mbox{if }(\forall i \{b_i=k\},
 +
\\f_k(B_L) + f_k(B_R), & \mbox{otherwise}
 +
\end{cases}
 +
</math>
 +
 +
где <math>f_0(x)</math> &ndash; первая цель; <math>f_0(x)</math> &ndash; вторая цель.
 +
 +
==== Задача коммивояжера ====
 
Задача коммивояжера (TSP)является наиболее известно из всего класса <math>NP</math>-сложных задач.
 
Задача коммивояжера (TSP)является наиболее известно из всего класса <math>NP</math>-сложных задач.
 
Формулируется задача следующим образом:  
 
Формулируется задача следующим образом:  

Версия 15:54, 20 июня 2012

Введение

В данной статье рассматривается многокритериальная оптимизация, её задача. Рассматривается понятие Парето-фронт - множество Парето оптимальных значений. Также рассматривается задача коммивояжера и предлагается алгоритм её мультиобъективизации

Задача многокритериальной оптимизации

Постановка задачи

Определение:
Задача многокритериальной оптимизации:
[math]maximize \{f(x) = (f_1(x),\dots,f_K(x))\}[/math]
[math] x \in X[/math]
где [math] f(x) : X \rightarrow R^K[/math] – целевая вектор-функция, где [math]K \ge 2[/math]

Так как не существует единого решение, которое было бы максимальным для всех целевых функций, вместо него можно искать множество [math]X^* \subseteq X [/math] множество Парето оптимальных значений.

Множество Парето оптимальных значений

Определение:
Множество Парето оптимальных значений:
[math]\forall x^* \in X^* \not\exists x \in X [/math]:[math]x \succ x^*[/math], где [math]x \succ x^* \Leftrightarrow (\forall i \in 1..K, (f_i(x) \ge f_i(x^*))\land (\exists i \in 1..K, f_i(x) \gt f_i(x^*)))[/math]

Выражение [math]x \succ x^*[/math] означает, что [math]x[/math] доминирует над [math]x^*[/math].

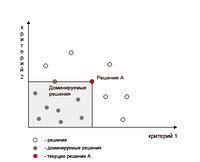
Говорят, что [math]x[/math] доминирует над [math]x^*[/math]. по Парето, если [math]x[/math] не хуже [math]x^*[/math] по всем критериям и хотя бы по одному критерию превосходит [math]x^*[/math]. В таком случае в выборе [math]x^*[/math] нет смысла, т.к. [math]x[/math] по всем параметрам не уступает, а по каким-то и превосхожит [math]x^*[/math]. Если рассматривать всего два критерия то на рис. 1 показана область пространства, доминируемая данным решением А. Эта область «замкнута»: элементы на ее границе также доминируемы А

Рис.1 – Доминируемые решения


Определение:
Для двух решений [math]x[/math] и [math]x'[/math] говорят [math]x \sim x'[/math] тогда и только тогда, когда [math]\exists i \in 1..K \colon f_i(x) \gt f_i(x') \land \exists j \in 1..K, j \ne i \colon f_j(x') \gt f_j(x)[/math] – такую пару решений называют недоминируемой

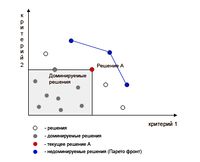
На рис. 2 показана граница Парето для возможных решений в двухкритериальном пространстве

Рис.2 – Парето фронт

Множество Парето оптимальных недоминируемых решений называется Парето фронтом.

Multi-objectivization

Суть метода мульти-объективизации заключается в разбитии сложной задачи с одной целевой функцией на несколько подзадач, найти для каждой подзадачи решение и выбрать оптимальное решение.

Для выполнения оптимизации многокритериальной задачи мы должны добавить в целевую функцию новые параметры, либо должны добавить новые целевые функции.

Сложность этой процедуры заключается в разложении проблемы на ряд мелких независимых между собой подпроблем.

Алгоритмы

Hill-Climbers

Определение:
Hill-Climbers – Итеративный алгоритм, который начинается с произвольного решения проблемы, а затем пытается найти лучшее решение, постепенно изменяя его. Если изменения позволяют найти лучшее решение, алгоритм сохраняет его и повторяет и повторяет своё выполнение до тех пор, пока лучшие решения не могут быть найдены


Initialization: [math]P \leftarrow \emptyset [/math]
Init_pop[math](P)[/math]
Main Loop: [math]x_1 \leftarrow [/math]Rand_mem[math](P)[/math],[math]x'_2 \leftarrow [/math]Rand_mem[math](P)[/math]

[math]x'_1 \leftarrow [/math]Mutate[math](P)[/math],[math]x_2 \leftarrow [/math]Mutate[math](P)[/math]
if[math](H(x_1,x'_1)+H(x_2,x'_2) \gt H(x_1,x'_2)+H(x_2,x'_1))[/math]

Swap[math](x_1,x'_2)[/math]

if [math]f(x'_1) \gt f(x_1)[/math]

[math]P \leftarrow P \cup x'_1 \setminus x_1[/math]

if [math]f(x'_2) \gt f(x_2)[/math]

[math]P \leftarrow P \cup x'_2 \setminus x_2[/math]
Termination: return Best[math](P)[/math]

Задачи

Hierarchical-if-and-only-if function

H-IIF – предназначена для моделирования проблемы с блочной структурой, каждый блок которой строго связан с остальными блоками.


[math] f(B)= \begin{cases}1,& \mbox{if } |B| = 1, \mbox{ else} \\|B|+f(B_L)+f(B_R),& \mbox{if }(\forall i \{b_i=0\} \mbox{ or } \forall i \{b_i = 1 \}) \\f(B_L) + f(B_R), & \mbox{otherwise} \end{cases} [/math],

где [math]B[/math] – блок бит [math]\{b_1,b_2,\dots,b_n \}, |B|[/math] – размер блока, а [math]B_L, B_R[/math] – левая и правая часть блока соответственно.

Применяя к этой задаче мультиобъективизацию, разобьём задачу [math]f[/math] на [math]k[/math]-задач.

Представим, как будет выглядеть [math]f(B)[/math]:

[math] f(B)= \begin{cases} 0, & \mbox{if } |B| = 1 \mbox{ and }b_1 \neq k, \mbox{ else} \\1,& \mbox{if } |B| = 1 \mbox{ and }b_1 = k, \mbox{ else} \\|B|+f_k(B_L)+f_k(B_R),& \mbox{if }(\forall i \{b_i=k\}, \\f_k(B_L) + f_k(B_R), & \mbox{otherwise} \end{cases} [/math]

где [math]f_0(x)[/math] – первая цель; [math]f_0(x)[/math] – вторая цель.

Задача коммивояжера

Задача коммивояжера (TSP)является наиболее известно из всего класса [math]NP[/math]-сложных задач. Формулируется задача следующим образом:

Задано [math]C=\{c_1,c_2,\dots,c_N\} [/math] – множество городов и для каждой пары [math]\{c_i,c_j\}[/math] задано расстояние. Наша цель – найти цепь из городов, минимизирующую величину:

[math]\sum^{N-1}_{i=1} d(C_{\pi(i)},C_{\pi(i+1)})+d(C_{\pi(N)},C_{\pi(1)})[/math]

Применяя к этой задаче мультиобъктивизацию, нужно разбить её на подзадачи. TSP – является [math]NP[/math]-сложной именно потому, что нет хорошего разложения этой задачи. Тем не менее задачу можно разбить на две или больше подтуров, каждый из которых мы можем минимизировать.

Представим подтуры в виде двух городов. Тогда наша задача примет вид:

[math]minimize\{f(\pi,a,b) = (f_1(\pi,a,b),f_2(\pi,a,b))\}[/math]
where[math]f_1(\pi,a,b)=\sum^{\pi^{-1}(b)-1}_{i=\pi^{-1}(a)} d(C_{\pi(i)},C_{\pi(i+1)})[/math]
and [math]f_2(\pi,a,b)=\sum^{N-1}_{i=\pi^{-1}(b)} d(C_{\pi(i)},C_{\pi(i+1)}) + \sum^{\pi^{-1}(a)-1}_{i=1} d(C_{\pi(i)},C_{\pi(i+1)}) [/math] [math]+ d(C_{\pi(N)},C_{\pi(1)})[/math],

где [math]a[/math] и [math]b[/math] – два города, указанных априори. Если [math]\pi (a) \lt \pi (b)[/math], меняем их местами.

Предполагается, что [math]a[/math] и [math]b[/math] выбраны произвольно.

Источники

Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Задача_многокритериальной_оптимизации._Multiobjectivization&oldid=26137»