QpmtnCmax

Эта статья находится в разработке!

Постановка задачи

Есть несколько станков с разной скоростью выполнения работ. Работу на каждом из станков можно прервать и продолжить позже.

Цель - выполнить все как можно быстрее.

1. Найдем нижнюю границу времени выполнения.

2. Составим оптимальное расписание.

Алгоритм построения расписания

[math] P_i = p_1 + ... + p_i[/math]

[math] S_j = s_1 + ... + s_j[/math]

Где [math]i = 1 ... n[/math]; [math]j = 1 ... m[/math]; [math] p_i[/math] - вес i-ой работы ;[math] s_j[/math] - скорость работы j-oй машины ; [math] n \ge m[/math];

Необходимое условие для выполнения всех работ в интервале [math][0;T][/math]:

[math] P_n = p_1 + ... + p_n \le s_1T + ... + s_mT = S_mT[/math] или [math]P_n/S_m \le T[/math]

Нижняя граница [math]C_{max}[/math] :

[math]w = \max\{\max\limits_{j=1}^{m-1} {P_i \over S_j}, {P_n \over S_m}\}[/math]

Будем назвать Level-ом работы [math] lvl(p_i(t)) [/math] - невыполненную часть работы [math] p_i [/math] в момент времени [math] t [/math]

Далее построим расписание, которое достигает нашей оценки [math]w[/math], с помощью Level-алгоритма.

Level - алгоритм:

  [math]t \leftarrow 0 [/math]
  WHILE существуют работы с положительным level
      Assign(t)
      [math]t1 \leftarrow min(s\gt t |[/math]работа выполненная в момент времени [math] s)[/math]
      [math]t2 \leftarrow [/math] найти минимальное s > t. Для которого выполняется для некоторых работ i , j:[math] level_i(t)\gt level_j(t)[/math] && [math]  level_i(s) == level_j(s))[/math]
      [math] t \leftarrow min(t1,t2) [/math]
  Построение расписания

Функция [math]Assign(t)[/math]:

  [math]J [/math] - множество работ с положительным level
  [math]M = \{M_1,...,M_m\}[/math] - множество всех станков
  WHILE ([math]J[/math] != 0 && [math]M[/math] != 0)
     Найти множество работ [math]I[/math] подмножество [math]J[/math] ,level которых максимальный
     [math]r \leftarrow min[/math](|[math]M[/math]|,|[math]I[/math]|)
     Назначаем работы из мн-ва [math]I[/math] на [math]r[/math] самых быстрых машин из мн-ва [math]M[/math]
     [math]J \leftarrow J[/math]\[math]I[/math]
     удаляем из мн-ва [math]M[/math] [math]r[/math] самых быстрых машин

Доказательство корректности алгоритма

Так как нижняя граница [math]C_{max}[/math]:

[math]w = \max\{\max\limits_{j=1}^{m-1} {P_i \over S_j}, {P_n \over S_m}\}[/math]

то достаточно показать, что составленное расписание достигает этой оценки.

Будем считать, что в начале алгоритма мы имеем [math] p_1(0) \ge p_2(0) \ge ... \ge p_n(0) [/math]. Это утверждение не меняется на протяжении всего выполнения алгоритма, для любого момента времени. Получаем: [math] p_1(t) \ge p_2(t) \ge ... \ge p_n(t) [/math]. Докажем что алгоритм составляет расписание в соответствии с этим свойством. Чтобы доказать этот факт, будем считать что в любой момент времени T нет простоев машин, когда есть хотя бы одна невыполненная работа. Получаем:

[math] T(s_1 + ... + s_m) = p_1 + p_2 + ... + p_n [/math] или [math] T = {P_n \over S_n} [/math]

Таким образом необходимая оценка достигается нашим алгоритмом.

Допустим хотя бы одна машина простаивает, в момент когда есть невыполненные работы, мы имеем следующее неравенство для времен окончания работ на станках [math]M_1 ... M_m[/math]:

[math] f_1 \ge f_2 \ge ... \ge f_m [/math]

В этом случае, если [math] f_i \lt f_{i+1} [/math] для некоторого [math] 1 \le i \le m-1 [/math], Level последней работы выполнявшейся на станке [math] M_i [/math] равен [math] f_i - \varepsilon [/math]. Где [math] \varepsilon \gt 0[/math] достаточно мал, и меньше чем Level последней работы на станке [math] M_{i+1} [/math]. Пришли к противоречию.

Пример

Картинка к примеру

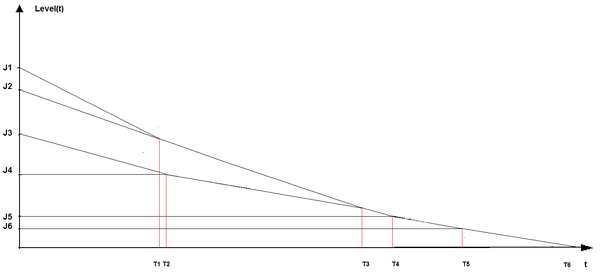
Пусть у нас есть 6 работ и 3 станка. Покажем работу алгоритма для данного случая.

В начальный момент времени начинаем обрабатывать работы с наибольшим временем выполнения [math]J_1-J_3[/math] на станках [math]M_1-M_3[/math] соответственно. В момент времени [math]T_1[/math] [math]lvl[/math] 1-ой работы и 2-ой работы совпадает. С этого момента начинаем обрабатывать работы [math] J_1,J_2[/math] синхронно на станках: [math]M_1 M_2[/math]. В момент времени [math]T_2[/math] работа [math]J_3[/math] опускается до уровня работы [math]J_4[/math].Работы [math] J_3,J_4[/math] выполняем одновременно на одном станке [math] M_3[/math]. В момент времени [math]T_3[/math] начинаем выполнять первые четыре работы на всех станках одновременно, далее просто добавятся работы [math]J_5 J_6[/math] и все работы закончатся одновременно.

Время работы

Level-алгоритм вызывает функцию Assign(t) в самом худшем случае [math]O(n)[/math] раз. Функция Assign(t) выполняется за [math]O(nm)[/math]. Итоговое время работы [math]O(n^2m)[/math].

Литература

• Peter Brucker. «Scheduling Algorithms» — «Springer», 2006 г. — 379 стр. — ISBN 978-3-540-69515-8