Z-функция

Определение

Z-функция от строки [math]S[/math] и позиции [math]x[/math] — это длина максимального префикса подстроки, начинающейся с позиции [math]x[/math] в строке [math]S[/math], который одновременно является и префиксом всей строки [math]S[/math]. Значение [math]Z[/math]-функции от первой позиции не определено, поэтому его обычно приравнивают к нулю или к длине строки.
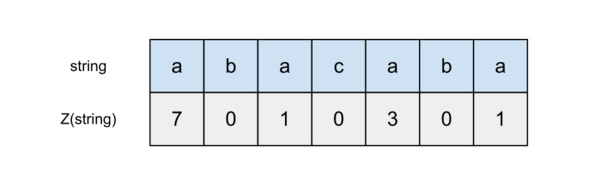
Примечание: далее в конспекте символы строки нумеруются с нуля.

Алгоритм поиска

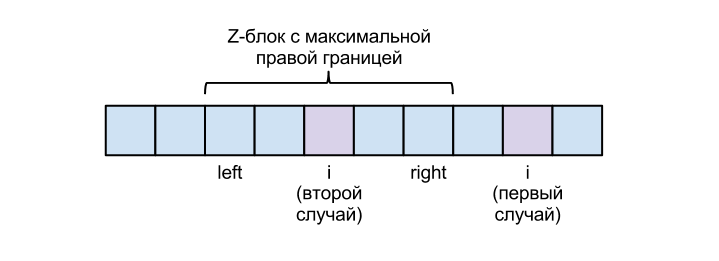
Z-блоком назовем подстроку с началом в позиции [math]i[/math] и длиной [math]Z[i][/math].
Для работы алгоритма заведём две переменные: [math]left[/math] и [math]right[/math] — начало и конец Z-блока строки [math]S[/math] с максимальной позицией конца [math]right[/math] (среди всех таких Z-блоков, если их несколько, выбирается наибольший). Изначально [math]left=0[/math] и [math]right=0[/math]. Пусть нам известны значения Z-функции от [math]0[/math] до [math]i-1[/math]. Найдём [math]Z[i][/math]. Рассмотрим два случая.

1) [math]i \gt right[/math]:
Просто пробегаемся по строке [math]S[/math] и сравниваем символы на позициях [math]S[i+j][/math] и [math]S[j][/math]. Пусть [math]j[/math] первая позиция в строке [math]S[/math] для которой не выполняется равенство [math]S[i+j] == S[j][/math], тогда [math]j[/math] это и Z-функция для позиции [math]i[/math]. Тогда [math]left = i, right = i + j - 1[/math]. В данном случае будет определено корректное значение [math]Z[i][/math] в силу того, что оно определяется наивно, путем сравнения с начальными символами строки.

2) [math]i \le right[/math]:
Сравним [math]Z[i - left] + i[/math] и [math]right[/math]. Если [math]right[/math] меньше, то надо просто наивно пробежаться по строке начиная с позиции [math]right[/math] и вычислить значение [math]Z[i][/math]. Корректность в таком случае также гарантированна. Иначе мы уже знаем верное значение [math]Z[i][/math], так как оно равно значению [math]Z[i - left][/math].

Время работы

Этот алгоритм работает за [math]O(\lvert S\rvert)[/math], так как каждая позиция пробегается не более двух раз: при попадании в диапазон от [math]left[/math] до [math]right[/math] и при высчитывании [math]Z[/math]-функции простым циклом.

Псевдокод

Zfunction(p) 
   answer[0] = 0
   left = 0
   right = 0
   for (i = 1..(n - 1))
      if (i > right)
         j = 0
         while (i + j < n && p[i + j] == p[j])
            j++
         answer[i] = j
         left = i
         right = i + j - 1
      else if (answer[i - left] < right - i + 1)
         answer[i] = answer[i - left]
      else 
         j = 1
         while (j + right < n && p[j + right - i] == p[right + j])
            j++
         answer[i] = right + j - i
         left = i
         right = right + j - 1
   return answer

Источники

Поиск подстроки и смежные вопросы — Хабр
Z-функция — Википедия