Алгоритм двух китайцев — различия между версиями
Yurik (обсуждение | вклад) |
Yurik (обсуждение | вклад) |
||
| Строка 20: | Строка 20: | ||
7) Полученное дерево <tex>T'</tex> — MST в графе <tex>G</tex>. | 7) Полученное дерево <tex>T'</tex> — MST в графе <tex>G</tex>. | ||
| − | == Корректность == | + | === Корректность === |
''' Замечания: ''' | ''' Замечания: ''' | ||
| Строка 36: | Строка 36: | ||
Из сделанных замечаний и леммы следует, что дерево <tex>T'</tex> — MST в <tex>G</tex>. | Из сделанных замечаний и леммы следует, что дерево <tex>T'</tex> — MST в <tex>G</tex>. | ||
| − | == Реализация == | + | === Реализация === |
лололол | лололол | ||
| Строка 43: | Строка 43: | ||
цв | цв | ||
| − | == Сложность == | + | === Сложность === |
Всего будет построено не более <tex>|V|</tex> конденсаций. Конденсацию можно построить за <tex>O(|E|)</tex>. Значит, алгоритм можно реализовать за <tex>O(|V||E|)</tex>. | Всего будет построено не более <tex>|V|</tex> конденсаций. Конденсацию можно построить за <tex>O(|E|)</tex>. Значит, алгоритм можно реализовать за <tex>O(|V||E|)</tex>. | ||
Версия 23:24, 10 декабря 2012
Алгоритм двух китайцев — алгоритм построения минимального остовного дерева во взвешенном ориентированном графе с корнем в заданной вершине. Был разработан математиками Чу Йонджином и Лю Цзенхонгом.
Содержание
Постановка задачи
Дан взвешенный ориентированный граф и начальная вершина . Требуется построить корневое остовное дерево в с корнем в вершине , сумма весов всех ребер которого минимальна.
Алгоритм
Описание
1) Если хотя бы одна вершина графа недостижима из , то требуемое дерево построить нельзя.
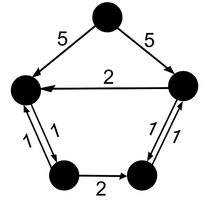
2) Для каждой вершины графа произведём следующую операцию: найдём ребро минимального веса, входящее в , и вычтем вес этого ребра из весов всех рёбер, входящих в . .
3) Строим граф , где — множество рёбер нулевого веса графа c весовой функцией . Если в этом графе найдётся остовное дерево с корнем в , то оно и будет искомым.
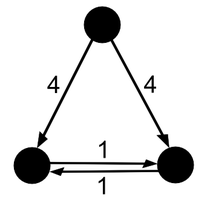
4) Если такого дерева нет, то построим граф — конденсацию графа . Пусть и — две вершины графа , отвечающие компонентам сильной связности и графа соответственно. Положим вес ребра между вершинами и равным минимальному среди весов рёбер графа с весовой функцией , идущих из в .
5) Продолжим с пункта 2, используя граф вместо .
6) В построено MST . Построим теперь MST в с весовой функцией . Добавим к все вершины компоненты сильной связности графа , которой принадлежит (по путям нулевого веса из ). Пусть в есть ребро , где отвечает компоненте сильной связности , а — компоненте сильной связности графа . Между и в графе с весовой функцией есть ребро , вес которого равен весу ребра . Добавим это ребро к дереву . Добавим к все вершины компоненты по путям нулевого веса из . Сделаем так для каждого ребра дерева .
7) Полученное дерево — MST в графе .
Корректность
Замечания:
- После перевзвешивания в каждую вершину, кроме , входит по крайней мере одно ребро нулевого веса.
- Пусть — искомое дерево в с весовой функцией . , т.е. - MST в с весовой функцией тогда и только тогда, когда — MST в с весовой функцией .
| Лемма: |
Кратчайшее дерево путей в графе можно получить, найдя кратчайшее дерево путей в графе , а затем заменив в нем каждую компоненту сильной связности деревом, построенным из дуг нулевой длинны. |
| Доказательство: |
| Зафиксируем любое дерево путей и покажем, что в графе найдется дерево не большей длины, имеющее такую структуру, как сказано в лемме. Для такой структуры дерева необходимо и достаточно, чтобы в каждое из подмножеств входило только по одному ребру. Меньше быть не может, иначе получится отдельная компонента связности. Если же в какое-то подмножество входит больше чем одно ребро, то все ребра кроме одного можно заменить ребрами нулевой длины, лежащими внутри подмножества, что разве лишь уменьшит длину дерева и не нарушит связности. Повторяя это преобразование нужное число раз мы добьемся искомой структуры дерева. |
Из сделанных замечаний и леммы следует, что дерево — MST в .
Реализация
лололол
цу
вц
цв
Сложность
Всего будет построено не более конденсаций. Конденсацию можно построить за . Значит, алгоритм можно реализовать за .
Источники
- Романовский И. В. Дискретный анализ, 3-е изд., перераб. и доп. - СПб.:Невский Диалект; БХВ-Петербург, 2003. - 320 с.: ил. - ISBN 5-7940-0114-3
- http://is.ifmo.ru