Алгоритм Ху-Таккера

Алгоритм Ху-Таккера - алгоритм построения оптимального алфавитного дерева.

Алфавитное дерево - дерево в котором при просмотре листьев слева направо символы идут в алфавитном порядке и код последующего лексикографически больше предыдущего.

Определение

Определение:

Пусть [math]A=\{a_{1},a_{2},...,a_{n}\}[/math] — алфавит из n различных символов, [math]W=\{w_{1},w_{2},...,w_{n}\}[/math] — соответствующий ему набор весов. Тогда алгоритм выбора набора бинарных кодов [math]C=\{c_{1},c_{2},...,c_{n}\}[/math], такой, что: 1. [math]c_{i}[/math] не является префиксом для [math]c_{j}[/math], при [math]i \ne j[/math] 2. для всех [math]a_{i}\lt a_{j}[/math], выполнено [math]c_{i}\lt c_{j}[/math] 3. при удовлетворенности условия 2, [math]\sum\limits_{i \in [1, n]} w_{i}\cdot |c_{i}|[/math] минимальна ([math]|c_{i}|[/math] — длина кода [math]c_{i}[/math]) называется алгоритмом Ху-Таккера.

Алгоритм

Изначально мы имеем только алфавит (и соответствующие веса) отсортированный лексикографически.

0. Введем следующие понятия. Две вершины называются совместимой парой, если они соседние или если между ними нет вершин алфавита. Две вершины называются минимальной парой, когда их суммарный вес наименьший из всех. При равенстве весов, выбирается пара с самой левой вершиной, из всех таких та у которой правый узел расположен левее. Минимальной совместимой парой называется наименьшая пара из всех совместимых.

1. Комбинирование. По данной последовательности из n вершин строим последовательность из [math]n-1[/math] вершины, комбинируя минимальную совместимую пару и заменяя ее левую вершину вершиной с весом [math] w = w_{l} + w_{r} [/math] и удаляя правую. Эта процедура повторяется до тех пор пока не останется одна вершина.

2. Определение уровней. Находим номер уровня [math]l_{i}[/math] каждого листа относительно корня.

3. Перестройка. После того, как номера уровней [math]l_{1}, l_{2}, ..., l_{n}[/math] всех листьев определены, просматриваем последовательность слева направо и находим самый левый среди максимальных номер уровня, скажем, [math]l_{i}=q[/math]. Тогда и [math]l_{i+1}=q[/math] (в последовательности [math]l_{1}, l_{2}, ..., l_{n}[/math] максимальные номера уровней всегда располагаются рядом). Создаем вершину уровня [math]q-1[/math] вместо вершин уровня [math]q[/math]. Другими словами, последовательность уровней [math]l_{1}, l_{2}, ..., l_{q}, l_{q}, ..., l_{n}[/math] заменяется на [math]l_{1}, l_{2}, ..., l_{q}-1, ..., l_{n}[/math]. Повторяем этот процесс до тех пор пока не останется одна вершина с уровнем 0.

Заметим, что перестройку легко можно организовать с помощью следующего стекового алгоритма.

Шаг 0. Стек пуст.

Шаг 1. Если значение двух верхних элементов различно или в стеке всего один элемент перейти к шагу 2, иначе шагу 3.

Шаг 2. Поместить следующий элемент [math]l_{i}[/math] на вершину стека.

Шаг 3. Удалить 2 верхних элемента стека, поместить в стек элемент со значением меньшим на единицу, чем удаленные, если значение нового элемента равно нулю - остановится, иначе перейти к шагу 1.

Пример

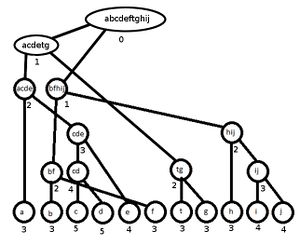
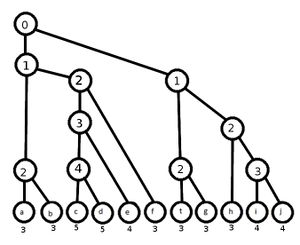
Для примера возьмем алфавит [math]A= \{[/math] a,b,c,d,e,f,t,g,h,i,j [math]\} [/math], а набор весов [math]W= \{[/math] 8,6,2,3,4,7,11,9,8,1,3 [math]\} [/math].

Выполним первый шаг алгоритма.

Объединим сначала [math]w(i)=1[/math] и [math]w(j)=3[/math], получим вершину с весом [math]w(ij)=4[/math], затем [math]w(c)=2[/math] и [math]w(d)=3[/math] на вершину веса [math]w(cd)=5[/math], и т.д. пока не останется одна вершина.

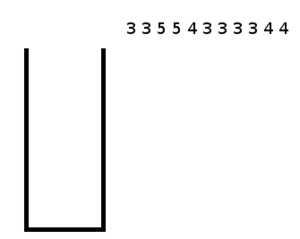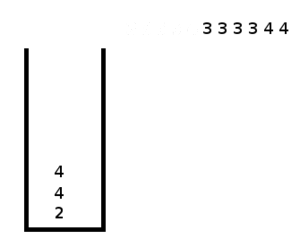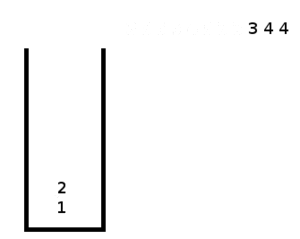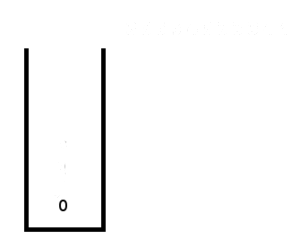
Выполним второй шаг.

Определим уровни для каждого листа [math]L= \{[/math] 3,3,5,5,4,3,3,3,3,4,4 [math]\} [/math].

Выполним третий шаг воспользовавшись стековым алгоритмом и получим необходимое дерево.

Осталось только назначить код для каждого символа, это делается аналогично коду Хаффмана, левым ребрам назначается 0, а правым 1.

Корректность алгоритма Ху-Таккера

Как пишет Д. Кнут короткого доказательства алгоритма не известно, и вероятно оно ни когда не будет найдено. Для доказательства своего алгоритма Ху и Таккеру потребовалось 3 теоремы и 2 леммы.

Сложность алгоритма

Для реализации данного алгоритма потребуется [math]O(n)[/math] памяти и [math]O(n \log n)[/math] времени на построение дерева.

Разберем оценку. Для доказательства такой оценки времени введем понятие локально минимальной совместимой пары (л.м.с.п), пара [math](w_{l},w_{r})[/math] является л.м.с.п, когда выполнены следующие условия [math]w_{r}\lt w_{i}[/math] для всех вершин [math]i[/math] совместимых с [math]l[/math] и [math]w_{l} \le w_{j}[/math] для всех вершин [math]j[/math] совместимых с [math]r[/math]. Так же докажем следующую лемму.

Лемма (1):

Пусть [math]a[/math] — любая вершина в последовательности, состоящей из вершин алфавита и вершин образованных в результате комбинации, [math]w_{i}[/math] — вес наименьшей вершины [math]i[/math], совместимой с [math]a[/math]. Если в результате комбинирования некоторой л.м.с.п. какая-нибудь новая вершина [math]d[/math] становится совместимой c [math]a[/math], то [math]w_{i}\lt w_{d}[/math] В частности, л.м.с.п. в последовательности вершин будет оставаться л.м.с.п., пока комбинируются другие л.м.с.п. Из этой леммы следует, что дерево, получаемое комбинированием л.м.с.п., не зависит от того, в каком порядке они комбинируются.

Доказательство:

[math]\triangleright[/math]

Рассмотрим произвольную вершину [math]a[/math] и предположим, что вес наименьшей вершины, совместимой с [math]a[/math], равен [math]w_{i}[/math]. Пусть комбинируется л.м.с.п. [math](b, c)[/math], причем [math]a[/math] ближе к [math]b[/math]. Тогда между [math]a[/math] и [math]b[/math] нет вершин алфавита и хотя бы одна из [math]b[/math], [math]c[/math] должна быть вершиной алфавита, иначе при слиянии [math](b, c)[/math] не появилось бы новых вершин (кроме [math]bc[/math]), совместимых с [math]a[/math]. Заметим, что [math]w_{i}[/math] может находиться в любой стороне от [math]a[/math]. Если вершина [math]w_{i}[/math] лежит справа от [math]a[/math], то она не вершина алфавита. Пусть [math]d[/math] — вершина, которая становится совместимой с [math]a[/math] после слияния [math](b, c)[/math] (она может быть как алфавитной так и слитой). Тогда [math]d[/math] должна быть совместима с [math]c[/math] в исходной последовательности и в силу локальной минимальности пары [math](b, c)[/math] имеем [math]w_{b} \le w_{d}[/math]. Но [math]w_{i}\lt w_{b}[/math], так как [math]b[/math] совместима с [math]a[/math] в исходной последовательности, а [math]w_{i}[/math] является наименьшим совместимым с [math]a[/math] весом. Поэтому [math]w_{i} \le w_{b} \le w_{d}[/math]. Мы доказали, что вес наименьшей вершины, совместимой с любой вершиной, не может уменьшиться. Отсюда следует, что любая л.м.с.п. [math](x, y)[/math] останется л.м.с.п. после слияния другой л.м.с.п., потому что [math]x[/math] останется наименьшей вершиной, совместимой с [math]y[/math], и наоборот.

[math]\triangleleft[/math]

Теперь согласно этой лемме нам не придется искать минимально совместимую пару, что весьма долго, достаточно лишь находить л.м.с.п. при этом не важно в каком порядке комбинировать л.м.с.п. По этому нам необходимо иметь массив размера [math]n[/math] из которого мы будем удалять л.м.с.п и создавать новую вершину, на нем легко будет осуществлять поиск л.м.с.п. А так же необходим массив размера [math]2n[/math] хранящий дерево, для реализации следующего шага. Второй шаг легко осуществить имея сохраненное дерево, проходом по дереву. Третий шаг реализованный стековым алгоритмом работает за [math]2n[/math] времени и необходимо [math]4n[/math] памяти, [math]n[/math] на стек, [math]n[/math] на хранения уровней вершин и [math]2n[/math] на хранение итогового дерева. Итак общая оценка как раз получается [math]O(n)[/math] памяти и [math]O(n \log n)[/math] времени.

Смотри также

• Алгоритм Хаффмана
• Избыточное кодирование, код Хэмминга

Литература

• Т.Ч.Ху и М.Т.Шинг Комбинаторные алгоритмы — стр. 166 — ISBN 5-85746-761-6
• Дональд Кнут Искусство программирования, том 3. Сортировка и поиск = The Art of Computer Programming, vol.3. Sorting and Searching. — 2-е изд. — М.: «Вильямс», 2007. — 824 с. — ISBN 5-8459-0082-4