Динамическое программирование по профилю — различия между версиями
Bear26 (обсуждение | вклад) (→Задача о замощении домино) |
Bear26 (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
'''Динамическое программирование по профилю''' <tex>-</tex> способ оптимизации перебора количества вариантов с помощью динамического программирования, когда одно из измерений не большое. | '''Динамическое программирование по профилю''' <tex>-</tex> способ оптимизации перебора количества вариантов с помощью динамического программирования, когда одно из измерений не большое. | ||
{{Определение | {{Определение | ||
| − | |definition='''Профиль''' - один из | + | |definition='''Профиль''' - один из столбцов(строк), удовлетворяющий условию задачи. Обычно используется в качестве состояния динамики. |
}} | }} | ||
== '''Задача о замощении домино''' == | == '''Задача о замощении домино''' == | ||
| − | Найти количество способов | + | Найти количество способов замостить таблицу <tex>n\times m</tex> с помощью доминошками размерами <tex>1\times 2,2\times 1</tex>. |
'''Решение:''' | '''Решение:''' | ||
| − | В качестве состояния динамики будем использовать | + | Для удобства можно хранить профили в виде двоичных масок. |
| + | В качестве состояния динамики будем использовать профили размерами n. В этом профиле 1 будет означать, что домино лежит горизонтально и заканчивается на этом столбце, иначе 0. Таких профилей будет <tex>2^n</tex>. | ||
Теперь проверим из какого профиля в какой можно перейти. | Теперь проверим из какого профиля в какой можно перейти. | ||
| Строка 21: | Строка 22: | ||
Пусть <tex>d[i][j] = 1</tex> если из профиля i можно перейти в j-ый, иначе 0. | Пусть <tex>d[i][j] = 1</tex> если из профиля i можно перейти в j-ый, иначе 0. | ||
| − | Пусть так же <tex>a[k][i]</tex> - количество способов замощения | + | Пусть так же <tex>a[k][i]</tex> - количество способов замощения первых k-1 столбцов и заканчивавшийся на i-ом профиле. |
Тогда <tex>a[k][i]=\displaystyle \sum_{j=0}^{2^n -1} a[k-1][j]\cdot d[j][i]</tex> | Тогда <tex>a[k][i]=\displaystyle \sum_{j=0}^{2^n -1} a[k-1][j]\cdot d[j][i]</tex> | ||
Ответом будет <tex> \sum a[m][i]</tex>, где i : профиль, который может быть последним (т.е. все группы из 0 имеют четные размеры) | Ответом будет <tex> \sum a[m][i]</tex>, где i : профиль, который может быть последним (т.е. все группы из 0 имеют четные размеры) | ||
| − | |||
| − | |||
'''Реализация''' | '''Реализация''' | ||
| Строка 63: | Строка 62: | ||
'''Решение:''' | '''Решение:''' | ||
| − | В качестве состояния динамики будем использовать | + | В качестве состояния динамики будем использовать профили размеров n. В этом профиле 1 будет означать что клетка закрашена в черный цвет, и 0 если в белый. |
Из профиля i в j-ый можно перейти если выполнено условие: | Из профиля i в j-ый можно перейти если выполнено условие: | ||
* если поставить i и j профиль рядом, то не должно быть квадратов <tex>2\times 2</tex> одного цвета | * если поставить i и j профиль рядом, то не должно быть квадратов <tex>2\times 2</tex> одного цвета | ||
Версия 18:54, 20 декабря 2012
Динамическое программирование по профилю способ оптимизации перебора количества вариантов с помощью динамического программирования, когда одно из измерений не большое.
| Определение: |
| Профиль - один из столбцов(строк), удовлетворяющий условию задачи. Обычно используется в качестве состояния динамики. |
Задача о замощении домино
Найти количество способов замостить таблицу с помощью доминошками размерами .
Решение: Для удобства можно хранить профили в виде двоичных масок. В качестве состояния динамики будем использовать профили размерами n. В этом профиле 1 будет означать, что домино лежит горизонтально и заканчивается на этом столбце, иначе 0. Таких профилей будет . Теперь проверим из какого профиля в какой можно перейти.
Из профиля i в профиль j можно перейти если выполняются условия:
- Можно положить горизонтальные домино. То есть там где в j профиле стоит 1, в i профиле должен стоять 0
- Можно доложить в оставшиеся клетки вертикальные домино. То есть оставшиеся 0 в i профиле должны образовывать четные подстроки.
Пусть если из профиля i можно перейти в j-ый, иначе 0.
Пусть так же - количество способов замощения первых k-1 столбцов и заканчивавшийся на i-ом профиле. Тогда
Ответом будет , где i : профиль, который может быть последним (т.е. все группы из 0 имеют четные размеры)
Реализация
//n, m размеры таблицы for i = 0..(1<<n)-1 for j = 0..(1<<n)-1 if можно перейти из i в j профиль d[i][j] = 1; else d[i][j] = 0; a[0][0] = 1; //Так как мы можем начать только с профиля где все клетки 0 for k = 1..m-1 for i = 0..(1<<n)-1 for j = 0..(1<<n)-1 a[k][i] += a[k-1][j] * d[j][i]; ans = 0; for i = 0..(1<<n)-1 if можно закончить i профилем ans += a[m-1][i]; return ans;
Оценка сложности : подсчет , и подсчет в итоге
Оценка памяти : , так же можно заметить что в массиве для k состояния нам нужно только k-1 состояние, при такой реализации нужно будет . Еще можно не считать массив d, а просто каждый раз перепроверять можем ли мы перейти в это состояние в итоге потребуется памяти, но нам потребуется больше времени , где время проверки возможности перехода из i в j, обычно проверка равна n и тогда время получается .
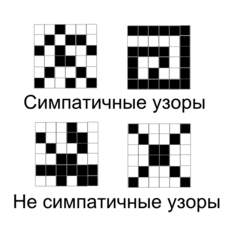
Задача о симпатичных узорах
Дана таблица , каждая клетка которой может быть окрашена в один из двух цветов: белый или черный. Симпатичным узором называется такая раскраска, при которой не существует квадрата , в котором все клетки одного цвета. Требуется найти количество симпатичных узоров для соответствующей таблицы.
Решение: В качестве состояния динамики будем использовать профили размеров n. В этом профиле 1 будет означать что клетка закрашена в черный цвет, и 0 если в белый. Из профиля i в j-ый можно перейти если выполнено условие:
- если поставить i и j профиль рядом, то не должно быть квадратов одного цвета
Пусть если из профиля i можно перейти в j-ый, иначе 0.
Пусть так же - количество способов раскрашивания первые k-1 столбцов и заканчивавшийся на i профиле. Тогда
Ответом будет
Для удобства можно хранить профиля в виде двоичных масок
Реализация:
//n, m размеры таблицы for i = 0..(1<<n)-1 for j = 0..(1<<n)-1 if можно перейти из i в j профиль d[i][j] = 1; else d[i][j] = 0; for i = 0..(1<<n)-1 a[i][0] = 1; //Так как мы можем начать c любого профиля for k = 1..m-1 for i = 0..(1<<n)-1 for j = 0..(1<<n)-1 a[k][i] += a[k-1][j] * d[j][i]; ans = 0; for i = 0..(1<<n)-1 ans += a[m-1][i]//Так как мы можем закончить любым профилем return ans;
Оценка сложности : подсчет , и подсчет в итоге
Оценка памяти : , так же можно заметить что в массиве для k состояния нам нужно только k-1 состояние, при такой реализации нужно будет . Еще можно не считать массив d, а просто каждый раз перепроверять можем ли мы перейти в это состояние в итоге потребуется памяти, но нам потребуется больше времени , где время проверки возможности перехода из i в j, обычно проверка равна n и тогда время получается .