Задача о рюкзаке

Задача о рюкзаке(англ. Knapsack problem) — дано [math]N[/math] предметов, [math]n_i[/math] предмет имеет массу [math] w_i \gt 0[/math] и стоимость [math] p_i \gt 0[/math]. Необходимо выбрать из этих предметов такой набор, чтобы суммарная масса не превосходила заданной величины [math]W[/math] (вместимость рюкзака), а суммарная стоимость была максимальна.

Формулировка задачи

Дано [math]N[/math] предметов, [math]W[/math] - вместимость рюкзака, [math]w=\{w_{1},w_{2},...,w_{N}\}[/math] — соответствующий ему набор положительных целых весов, [math]p=\{p_{1},p_{2},...,p_{N}\}[/math] — соответствующий ему набор положительных целых стоимостей. Нужно найти набор бинарных величин [math]B=\{b_{1},b_{2},...,b_{N}\}[/math], где [math]b_{i} = 1 [/math], если предмет [math]n_i[/math] включен в набор, [math] b_{i} = 0 [/math], если предмет [math]n_i[/math] не включен, и такой что:

1. [math]b_{1} w_{1}+ ... + b_{N} w_{N} \le W[/math]
2. [math]b_{1} p_{1}+ ... + b_{N} p_{N} [/math] максимальна.

Варианты решения

Задачу о рюкзаке можно решить несколькими способами:

• Перебирать все подмножества набора из N предметов. Сложность такого решения [math]O({2^{N}})[/math].

• Методом Meet-in-the-middle. Сложность решения [math] O({2^{N/2}}\times{N}) [/math]

• Метод динамического программирования. Сложность - [math]O(N \times W)[/math].

Метод динамического программирования

Пусть [math]A(k, s)[/math] есть максимальная стоимости предметов, которые можно уложить в рюкзак вместимости [math]s[/math], если можно использовать только первые [math]k[/math] предметов, то есть [math]\{n_1,n_2,...,n_k\}[/math], назовем этот набор допустимых предметов для [math]A(k,s)[/math].

[math]A(k, 0) = 0[/math]

[math]A(0, s) = 0[/math]

Найдем [math]A(k, s)[/math]. Возможны 2 варианта:

1. Если предмет [math]k[/math] не попал в рюкзак. Тогда [math]A(k, s)[/math] равно максимальной стоимости рюкзака с такой же вместимостью и набором допустимых предметов [math]\{n_1,n_2,...,n_{k-1}\}[/math], то есть [math]A(k,s) = A(k-1, s)[/math]
2. Если [math]k[/math] попал в рюкзак. Тогда [math]A(k, s)[/math] равно максимальной стоимости рюкзака, где вес [math]s[/math] уменьшаем на вес [math]k[/math] -ого предмета и набор допустимых предметов [math]\{n_1,n_2,...,n_{k-1}\}[/math] плюс стоимость [math]k[/math], то есть [math]A(k-1, s-w_k) + p_k[/math]

Если короче:

1. [math]A(k,s) = A(k-1, s)[/math]
2. [math]A(k,s) = A(k-1, s-w_k) + p_k[/math]

Выберем из этих двух значений максимальное:

[math]A(k,s) = max(A(k-1,s), A(k-1,s-w_{k}) + p_{k})[/math]

Стоимость искомого набора равна [math]A(N,W)[/math], так как нужно найти максимальную стоимость рюкзака, где все предметы допустимы и вместимость рюкзака [math]W[/math].

Восстановим набор предметов, входящих в рюкзак

Будем определять входит ли [math]n_i[/math] предмет в искомый набор. Начинаем с элемента [math]A(i,w)[/math], где [math]i = N[/math], [math]w = W[/math]. Для этого сравниваем [math]A(i,w)[/math] со следующими значениями:

1. Максимальная стоимость рюкзака с такой же вместимостью и набором допустимых предметов [math]\{n_1,n_2,...,n_{i-1}\}[/math], то есть [math]A(i-1, w)[/math]
2. Максимальная стоимость рюкзака с вместимостью на [math]w_i[/math] меньше и набором допустимых предметов [math]\{n_1,n_2,...,n_{i-1}\}[/math] плюс стоимость [math]p_i[/math], то есть [math]A(i-1, w-w_i)+p_i[/math]

Заметим, что при построении [math]A[/math] мы выбирали максимум из этих значений и записывали в [math]A(i, w)[/math]. Тогда будем сравнивать [math]A(i, w)[/math] c [math]A(i-1, w)[/math], если равны, тогда [math]n_i[/math] не входит в искомый набор, иначе входит.

Реализация

Сначала генерируем [math]A[/math].

for i = 0..W
  A[0][i] = 0
for i = 0..N
  A[i][0] = 0    //Первые элементы приравниваем 0
for k = 1..N               
  for s = 0..W   //Перебираем для каждого k, все вместисмости 
    if s >= w[k]    //Если текущий предмет вмещается в рюкзак
      A[k][s] = max(A[k-1][s], A[k-1][s-w[k]]+p[k]) //выбираем класть его или нет
    else 
      A[k][s] = A[k-1][s]             //иначе, не кладем

Затем найдем набор [math]ans[/math] предметов, входящих в рюкзак, рекурсивной функцией:

findAns(k, s)
  if A[k][s] == 0 
    return
  if A[k-1][s] == A[k][s]
    findAns(k-1, s)
  else 
    findAns(k-1, s - w[k]);
    ans.push(k);

Сложность алгоритма [math]O(N \times W)[/math]

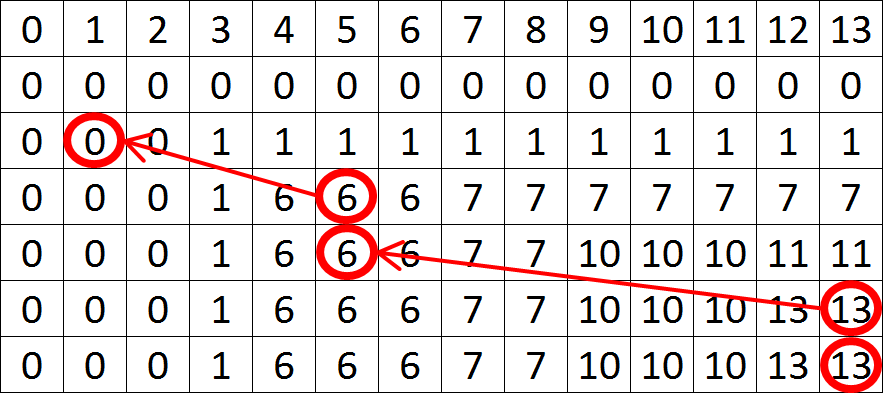
Пример

[math]W = 13, N = 5[/math]

[math]w_{1} = 3, p_{1} = 1 [/math]

[math]w_{2} = 4, p_{2} = 6 [/math]

[math]w_{3} = 5, p_{3} = 4 [/math]

[math]w_{4} = 8, p_{4} = 7 [/math]

[math]w_{5} = 9, p_{5} = 6 [/math]

	0	1	2	3	4	5	6	7	8	9	10	11	12	13
k = 0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
k = 1	0	0	0	1	1	1	1	1	1	1	1	1	1	1
k = 2	0	0	0	1	6	6	6	7	7	7	7	7	7	7
k = 3	0	0	0	1	6	6	6	7	7	10	10	10	11	11
k = 4	0	0	0	1	6	6	6	7	7	10	10	10	13	13
k = 5	0	0	0	1	6	6	6	7	7	10	10	10	13	13

Числа от 0 до 13 в первой строчке обозначают вместимость рюкзака.

В первой строке как только вместимость рюкзака [math]n \ge 3[/math], добавляем в рюкзак 1 предмет.

Рассмотрим [math]k = 3[/math], при каждом [math]s \ge 5 ([/math]так как [math]w_3 = 5)[/math] сравниваем [math]A[k-1][s][/math] и [math]A[k-1][s-w_3]+p_3[/math] и записываем в [math]A[k][s][/math] стоимость либо рюкзака без третьего предмета, но с таким же весом, либо с третьим предметом, тогда стоимость равна стоимоси третьего предмета плюс стоимость рюкзака с вместимостью на [math]w_3[/math] меньше.

Максимальная стоимость рюкзака находится в [math]A(5, 13)[/math].

Восстановление набора предметов, из которых состоит максимально дорогой рюкзак.

Начиная с [math]A(5, 13)[/math] восстанавливаем ответ.

Таким образом, в набор входит [math]2[/math] и [math]4[/math] предмет.

Стоимость рюкзака [math]= 6 + 7 = 13[/math]

Вес рюкзака [math]= 4 + 8 = 12[/math]

Другие задачи семейства

Ограниченый рюкзак

Ограниченый рюкзак (англ. Bounded Knapsack Problem) - обобщение классической задачи, когда любой предмет может быть взят некоторое количество раз.

Формулировка Задачи

Каждый предмет может быть выбран ограниченное [math]b_i[/math] число раз. Задача выбрать число [math]x_i[/math] предметов каждого типа так, чтобы

максимизировать общую стоимость: [math]\sum_{i=1}^N p_ix_i[/math]

выполнялось условие на совместность: [math]\sum_{i=1}^N w_ix_i \le W[/math]

и [math] x_i \in (0,1,...,b_i)[/math] для всех [math] i= 1,2,...,N[/math]

Варианты решения

При небольших [math]b_i[/math] решается сведением к классической задаче о рюкзаке. В иных случаях:

• Методом ветвей и границ
• Методом динамического программирования

Метод динамического программирования

Пусть [math]d(i,c)[/math] максимальная стоимость любого возможного числа предметов типов от 1 до [math]i[/math], суммарным весом до [math]c[/math].

Заполним [math]d(0,c)[/math] нулями.

Тогда меняя i от 1 до [math]N[/math], расчитаем на каждом шаге [math]c[/math] от 0 до [math]W[/math] по рекурентной формуле:

[math]d(i,c) = max(d(i - 1, c - lw_i) + lp_i : l\ integer[/math] [math]0 \le l \le min(b_i,\lfloor c/w_i \rfloor))[/math]

Если не нужно востанавливать ответ, то можно использовать одномерный массив [math]d(c)[/math] вместо двумерного.

После выполнения в [math] d(N,W) [/math] будет лежать максимальная стоимость предметов, помещающихся в рюкзак.

Сложность алгоритма [math]O(NW^2)[/math].

Не ограниченный рюкзак

Не ограниченный рюкзак (англ.Unbounded Knapsack Proble) - обобщение ограниченого рюкзака, в котором любой предмет может быть выбран любое количество раз.

Формулировка Задачи

Каждый предмет может быть выбран любое число раз. Задача выбрать количество [math]x_i[/math] предметов каждого типа так, чтобы

максимизировать общую стоимость: [math]\sum_{i=1}^N p_ix_i[/math]

выполнялось условие на совместность: [math]\sum_{i=1}^N w_ix_i \le W[/math]

[math] x_i \ge 0 [/math] целое, для всех [math] i= 1,2,...,N[/math]

Варианты решения

Самые распространенные методы точного решения это:

• Метод ветвей и границ
• Метод динамического программирования

Метод динамического программирования

Пусть [math]d(i,c)[/math] максимальная стоимость любого количества вещей типов от 1 до [math]i[/math], суммарным весом до [math]c[/math] включительно.

Заполним [math]d(0,c)[/math] нулями.

Тогда меняя i от 1 до [math]N[/math], расчитаем на каждом шаге [math]c[/math] от 0 до [math]W[/math] по рекурентной формуле:

[math] d(i,c) = \begin{cases} d(i - 1, c) & for\ c = 0, ..., w_i - 1; \\ max(d(i - 1, c), d(i, c - w_i) + p_i) & for\ c = w_i, ..., W; \end{cases} [/math]

Если не нужно востанавливать ответ, то можно использовать одномерный массив [math]d(c)[/math] вместо двумерного, и использовать формулу:

[math] d(c) = max(d(c), d(c - w_i) + p_i) [/math]

После выполнения в [math] d(N,W) [/math] будет лежать максимальная стоимость предметов, помещающихся в рюкзак.

Сложность алгоритма [math]O(NW)[/math].

Непрерывный рюкзак

Непрерывный рюкзак (англ. Continuous knapsack problem) - вариант задачи, в котором возможно брать любою дробную часть от предмета, при этом удельная стоимость сохраняется.

Формулировка Задачи

Задача выбрать часть [math]x_i[/math] каждого предмета так, чтобы

максимизировать общую стоимость: [math]\sum_{i=1}^N p_ix_i[/math]

выполнялось условие на совместность: [math]\sum_{i=1}^N w_ix_i \le W[/math]

[math] 0 \le x_i \le 1[/math] дробное, для всех [math] i= 1,2,...,N[/math]

Варианты решения

Изменение формулировки значительно облегчает задачу. Жадный алгоритм дает оптимальное решение в данном случае.

Задача о суммах подмножеств

Задача о суммах подмножеств (англ. Subset-sum problem, Value Independent Knapsack Problem) - задача из семейства, в которой стоимость предмета совпадает с его весом.

Формулировка Задачи

Нужно выбрать подмножество так, чтобы сумма ближе всего к [math]W[/math], но не превысила его. Более формально, нужно найти набор бинарных величин [math]x_i[/math], так чтобы

максимизировать общую стоимость: [math]\sum_{i=1}^N w_ix_i[/math]

выполнялось условие на совместность: [math]\sum_{i=1}^N w_ix_i \le W[/math]

[math] x_i \ge 0 [/math] целое, для всех [math] i= 1,2,...,N[/math]

Варианты решения

Для решения пригодны любые методы для классической задачи, однако специализированые алгоритмы, обычно более оптимальны по параметрам. Используется:

• Метод динамического программирования
• Гибридный метод на основе динамического программирования и поиска по дереву. [math] O(n) [/math] в худшем случае.

Метод динамического программирования

Пусть [math]d(i,c)[/math] максимальная сумма [math]\le c[/math], подмножества взятого из [math] 1, ...,\ i[/math] элементов.

Заполним [math]d(0,c)[/math] нулями.

Тогда меняя i от 1 до [math]N[/math], расчитаем на каждом шаге [math]c[/math] от 0 до [math]W[/math] по рекурентной формуле:

[math] d(i,c) = \begin{cases} d(i - 1, c) & for\ c = 0, ..., w_i - 1; \\ max(d(i - 1, c), d(i - 1, c - w_i) + w_i) & for\ c = w_i, ..., W; \end{cases} [/math]

После выполнения в [math] d(N,W) [/math] будет лежать максимальная сумма подмножества, не превышающая заданное значение.

Сложность алгоритма [math]O(NW)[/math].

Задача о размене

Задача о размене' (англ. "") - обобщение ограниченого рюкзака, в котором любой предмет может быть выбран любое количество раз.

Формулировка Задачи

Каждый предмет может быть выбран любое число раз. Задача выбрать количество [math]x_i[/math] предметов каждого типа так, чтобы

максимизировать общую стоимость: [math]\sum_{i=1}^N p_ix_i[/math]

выполнялось условие на совместность: [math]\sum_{i=1}^N w_ix_i \le W[/math]

[math] x_i \in {0,1} [/math], для всех [math] i= 1,2,...,N[/math]

Варианты решения

Самые распространенные методы точного решения это:

• Метод ветвей и границ
• Метод динамического программирования

Метод динамического программирования

Пусть [math]d(i,c)[/math] максимальная стоимость любого количества вещей типов от 1 до [math]i[/math], суммарным весом до [math]c[/math] включительно .

Заполним [math]d(0,c)[/math] нулями.

Тогда меняя i от 1 до [math]N[/math], расчитаем на каждом шаге [math]c[/math] от 0 до [math]W[/math] по рекурентной формуле:

[math] d(i,c) = \begin{cases} d(i - 1, c) & for\ c = 0, ..., w_i; \\ max(d(i - 1, c), d(i, c - w_i) + p_i) & for\ c = w_i, ..., W; \end{cases} [/math]

Если не нужно востанавливать ответ, то можно использовать одномерный массив [math]d(c)[/math] вместо двумерного, и использовать формулу:

[math] d(c) = max(d(c), d(c - w_i) + p_i) [/math]

После выполнения в [math] d(N,W) [/math] будет лежать максимальная стоимость предметов, помещающихся в рюкзак.

Сложность алгоритма [math]O(NW)[/math].

Литература

• Дистанционная подготовка по информатике
• Код для нескольких задач семейства на всевозможных языках
• David Pisinger Knapsack problems. — 1995
• Knapsack Problems: Algorithms and Computer Implementations. Silvano Martello, Paolo Toth.